京都観光のガイドブログです。定番の楽しみ方から特別拝観、さらには年に1度の御開帳まで。
京都観光では最も詳しいです!
Amadeusの「京都のおすすめ」 ブログ版(観光)
長男Kくんの数学定期テスト対策の問題
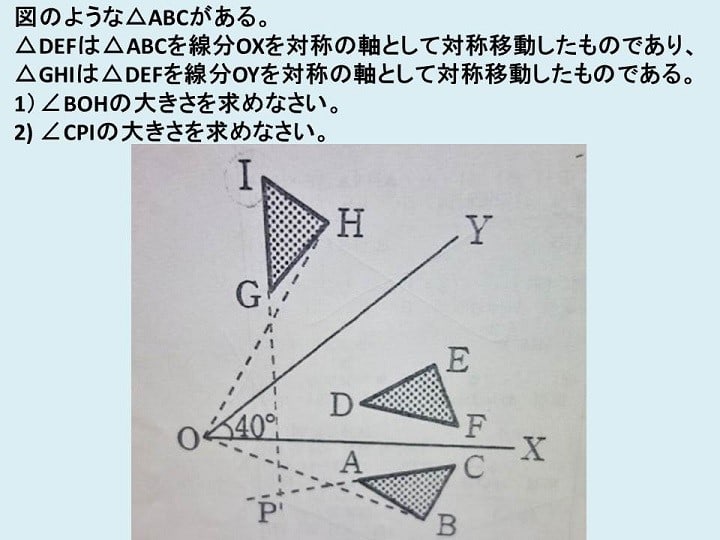
今夜は長男くんのお話。
彼は4月から洛星中学に通学しており、明日で最初の定期考査が終わります。
そんな中、先日彼の友人から「テスト範囲のこの問題の(2)出来た?」と、TELがあったそうです。
しかしKくんもすぐには分からなかったらしく、僕が帰宅したら妻から「これ、分かる~~~?」と聞いてきました。
学校のテキストの問題ですが、答えの数字はあるものの解法が書いていない。
まあ「自分で考えろ」ってことなんでしょう。
Kくんも友人もまわりの大人も出来ないよう。
そこで満を持して!?、僕の出番ですw
メンサのプライド、旧帝医卒のプライド、そして何より「中高は勉強しかした記憶がないという残念な過去」を否定しないためにも、絶対に引き下がれないところです(笑)!
さてまずは(1)。
これは簡単。
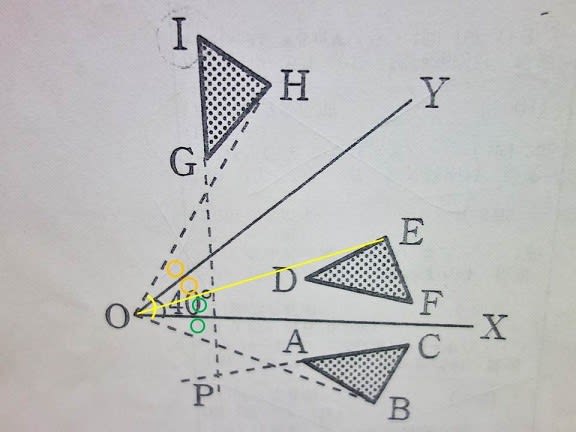
上図のようにOEに補助線を引くと、
OXでの線対称で、〇が一緒。
OYでの線対称で、〇が一緒。
〇+〇=40度なので、
∠BOH=2〇+2〇=80°となります。
まあこれは中学受験をしていれば、問題なく解けるでしょう。
問題の(2)です。
まずはスタート地点(与えられた条件)から。
角度を問われている問題で、与えられた角度が40度だけなので、これと絡めて解くハズ
線対称が2つあるので、(1)での補助線OEの左右で合同な三角形が2組出来るので、この辺りは使うだろう
というのは分かりますが、そこから先が・・・。
そこで今度はゴール地点(求めたい答え)から逆算します。

(1)から、)は80度と分かっている。
→欲しい )は、どうも80度っぽい。
→それを証明するには、青の三角形2つが相似と言えればよい
→ )は対頂角で同じ
→よって、〇=〇と言えればよい
ここまで、問題を変換することが出来ました。

角度が同じことを証明するのに、まだ使っていない線対称を使うハズということで、
まず
〇は対頂角で、上と一緒
→上の〇は、OYの線対称で〇と一緒
→〇は、OXの線対称で〇と一緒
→〇は、対頂角で〇と一緒
→よって〇=〇と言えました。
これで解けましたね。
解答としては、これをアタマから考えたように書くだけ。
解答
対頂角で、〇=〇
OXの線対称で〇=〇
OYの線対称で〇=〇
対頂角で〇は下の角と一緒
)は対頂角で一緒なので、〇=〇と併せて青の三角形は相似
よって、∠CPI=∠BOH=80度
もう現役を引退して30年弱になりますが、なんとか面目躍如出来ましたw
まあ僕が解けたのはいいんですが、Kくんももうちょっと1問を諦めずに粘らないと。
定期テスト中はそんな時間はないので、「普段の勉強からそうした姿勢で臨んで欲しい」と言っておきました。
「京都のおすすめ」の総合索引へ
コメント ( 2 ) | Trackback ( )
 -泥棒除け(著作権保護)12月12日の逆さ札
——
-泥棒除け(著作権保護)12月12日の逆さ札
——
 -火伏せ・防火(ブログ炎上防止)”火迺要慎(ひのようじん)”のお札—
---------------
-このブログの見方
22:00に自動更新。
-
22:00は拝観報告。
--タイトルに訪問日時が入っているもの。--
内容は最近の拝観の--主観的な感想です。
----------------------
拝観報告がない時は、本編。
----------------タイトルが神社仏閣の名前だけのもの。-
内容は神社仏閣の拝観の客観的な解説です。
-火伏せ・防火(ブログ炎上防止)”火迺要慎(ひのようじん)”のお札—
---------------
-このブログの見方
22:00に自動更新。
-
22:00は拝観報告。
--タイトルに訪問日時が入っているもの。--
内容は最近の拝観の--主観的な感想です。
----------------------
拝観報告がない時は、本編。
----------------タイトルが神社仏閣の名前だけのもの。-
内容は神社仏閣の拝観の客観的な解説です。