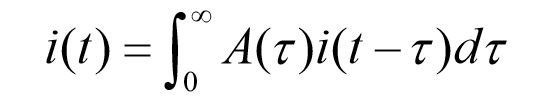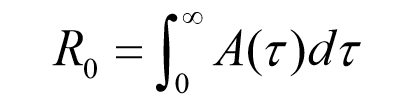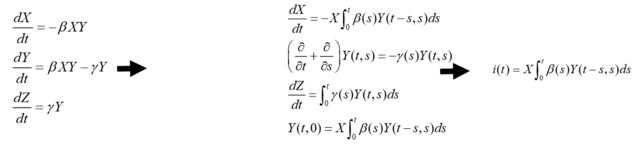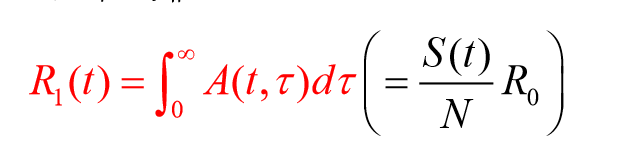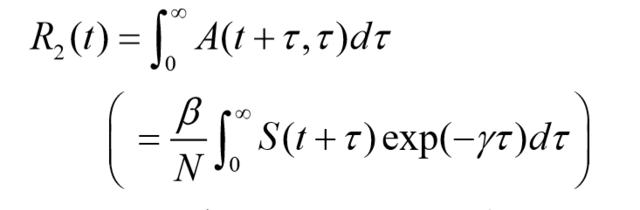 【8割おじさん西浦教授に聞く】新型コロナの実効再生産数のすべて オンライン講演会生中継/主催:日本科学技術ジャーナリスト会議
【8割おじさん西浦教授に聞く】新型コロナの実効再生産数のすべて オンライン講演会生中継/主催:日本科学技術ジャーナリスト会議
https://live2.nicovideo.jp/watch/lv325833316
について、やっとメモできたので、メモメモ
(以下の数式は、github
https://github.com/contactmodel/COVID19-Japan-Reff/nishiura_Rt会議_12May2020.pdf
から引用)
■ごあいさつ
■ファシリテーターから
・趣旨説明
「科学的助言」 東日本大震災でもあったが、これまでと違う
→専門家の顔が見える(いままで 政府:御用学者)
どう扱っていい?政治家、官僚、メディアも困惑
提言と違うじゃないか?→健全なこと
背景が見えるようになる
オープンサイエンス
今回はあくまで北海道大学の西浦先生がJASTJの勉強会で語る
→政府のクラスター班ではなく・・
タイトルの「すべて」は盛りすぎです。
第一部 講演
第二部 代表質問(江島先生 インディアナ大学)
第三部 質疑応答
■第一部 講演「実行再生産数とその周辺」
・背景にある理論、実装、問題を話す
・githubに今日のスライド、データセット、Rコードある
https://github.com/contactmodel/COVID19-Japan-Reff
・研究員
今日の分析
MCMC,R STANを使っている
公開していいデータ
・高校理系数学以上のバックグラウンドを想定
・個人として発表(クラスター班反映してない)
・基本再生産数
R0 0一番最初、
ばーじんそいる(みんなが感染しうる)集団において
1人の感染者が生み出す二次感染者数の平均値と解釈できる数値
あーるぜろ→あーるのーと(ぬるのはせい)
フォーマルに
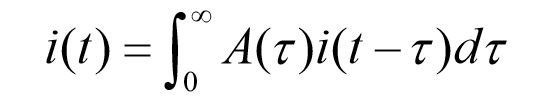
i(t)あいおぶてぃ:t時の新規感染者数
i(t-τ)あいおぶてぃまいなすたう:過去の(t-τ)時の感染者数
A(τ):二次感染の割合
τ:感染後経過時刻
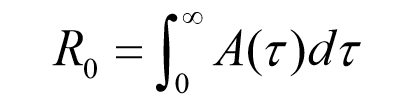
全てのプロセスを通じて二次感染者が出た割合→R0
数理的に出てくる
・流行の増殖期
Ro本質的に数理的
実践性として定量化しやすいものが必要→実行再生産数
人口学でも使われる
Rn:ねっとりぷろだくとれーしお
・実行再生産数:R0じゃないときのR0っぽいのをReと言っている
主に4つ
今回AとDの意味合いを込めたD
再生産方程式

下に書いてあるのはSIRモデル
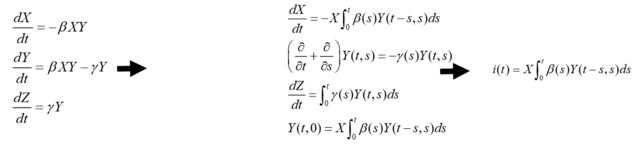
できるだけ一般的に
1人当たり
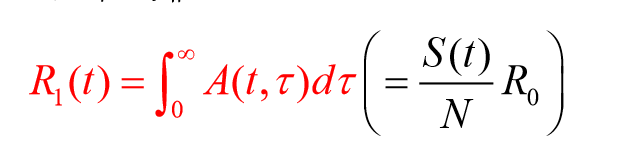
R(t)はA(t,τ)をτで積分(S(t)/NRo)
人口学だとピリオド合計特殊出生率に相当
→流行対策の評価:ピリオドの評価が適している
二次感染者数の平均
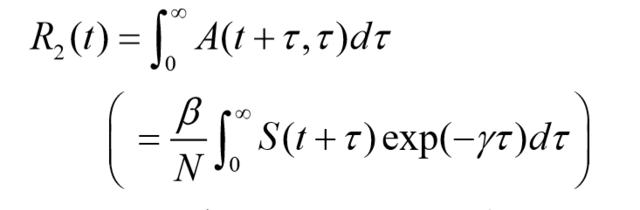
R(t)はA(t+τ,τ)→τを前向きに積分(S(t)/NRo)
人口学では、コホート合計出生率
・Rt<1
1を下回ると、新規感染者数が減っているといえる
落とし穴ある:流行のメカニズム→再感染がある場合など
(1以下でも安定化委がある可能性:そういう病気は知ってる限りないが。。。)
・単純化されたケース
3日間で次の世代に移り変わる
→3日ごとの比を取れば、E(Rn)
実際にはカレンダー日付でいくつもの世代
デイリーのどう対応
再生産方程式

A(t,τ)をR(t)g(τ) R(t)と、のこりのτの部分を出しg(t)とする
g(t)既知と想定:世代時間(の確率密度)→発病間隔(の確率密度)
発病間隔
発病してから二次感染の発病までの時間→感染から感染までとざっくり同じ
・観察データの問題
感染イベント 時刻わからない 潜伏期間
発病 少しわかる 診断の遅れ
診断 報告されたらわかる 報告の遅れ
2週間遅れてプレスデータへ
→受診の目安などかかわってる 発病後4日間診断されない
・流行の対策を知るのは感染日を知りたい・・・けど見れない
→逆計算する
C1,2,3,4 1日目、2日目・・・の発病者
i 感染者
fo 発病する確率(感染者X発病する確率・・・発病した人)
→畳み込み(1日、2日・・・を全部足す)する
・毎日の感染者数が分かっているので、
積分でなく挿話にして
ポアソン分布
→Rではサーベイランスとしてパッケージ化
スムージングする(イーブンNoで)
・日本のデータ
逆計算の問題だけではない
発病日、確定日:ずいぶんサイズちがう(どちらもわからない人も)
報告の遅れもある
3月の後半から発病時刻が東京抜けている
ボランティア班で今回は作っている
国立感染症研究所のサーベイランスが公式
分析は2パターン
発病時刻既知の人
確定日が分かっている人→感染時刻推定も
・Rtの推定
E:期待値
iドメスティック:国内
iトータル:国内国外全部
F:報告の遅れを加味(累積 畳み込み)
MCMCを用いて推定
後日:報告の遅れありうる→東京
18日前にデータをトランケートしている
→リアルタイム性に乏しい
・対応できていない
インピュテーション
年齢別、空間
リンクのある人(接触歴)とそうでない人
・R(t)が「いつのまにか」倍加時間で評価
C(t)=C(0)2^1/Td
→オーバーシュートを可能な限りふせぐため
R(t)はバックワード
ダブリングタイムは増えているとき
→患者が増加しているときはダブリングタイム
ダブリングタイムをしっかり見ないといけない
北海道:2段になっているとき→リアルタイムにみている
(1回累積をリセットする)
・R(t)について、どうしていくべきか(私見)
ダッシュボード
カンマーアンドダンス減ってから増える→Rtのアップデート
R(t)のリアルタイム性
でぃすぱーしびりてぃーれーしお X これくてぃんぐふぁくたー
→たとえば、
直近7日間の患者数 < その前の7日間の患者数
(精密な情報失う、報告の著しい遅れの場合)
・R(t)のまとめ
非定常状態での流行増減の記述(ダイナミックに起こる)
R0と一定の関係
増えているか否か、スピードがわかる
万能ではない
■第二部 代表質問
・スムージングをしてとは何のこと?
感染時刻の逆計算をノンパラメトリックでやっています。
C:患者数 iの感染者数推定
単なる最尤推定だと、でこぼこになる
→EMあるごりずむを使う:スムージングしている
→パッケージングに実装されている。
スムージングパラメーターを指定する(偶数でないといけない)
次第に挙げて推定
・R(t)の推定へ
Iが観察データ、Eが期待値(モデル)
・全部を補足できていない
(1)確定患者は氷山の一角?感染者全員ではないのでは?
ふけんせいかんせい
→j(t)=ki(t)
J感染者 k何倍か i 感染者
Jはiをk倍したものなので、再生産方程式は使える
(2)時刻とともに変わる場合
→ピーク付近が過小評価
q(t) 入院比率などで修正できる PCR件数:あんまりかわっていない
→2とおりのインピュテーション問題
■第三部
・誤植について(上下逆だった)
・世代時間 長いと想定すれば、再生産数は大きくなる
分散は大きくなると小さくなる
もともとのシリアルインターバル 香港大学の武漢の観察
平均6日より長い
SARS 8.なんにちか シンガポールの家庭内
似て非なる特徴 感染の怒り方の違い
SARS 肺炎が起こる前後に二次感染→病院伝播がおおい
自分自身で4.8と出した→サンプル数多くない
今アップデート
R(t)としての推定:起こりえる 誠実な対応としては感度分析
オリジナルで研究をやっていたので、今回使ったが、
感度分析を
日本のシリアルインターバル:東北大学で研究中
ホストの異質性も加味したうえで推定(場)
・逆計算で死亡とか回復は入れなくていいの?
→加味しないでいい
・非定常ポアソン過程
SIRモデルを微分方程式:ばらつき考慮していない
→ポアソン過程 バリエーションを無視した場合
時刻とともにすそ野の長いようなとき
→確率的揺らぎの場合、二項分布でキャプチャしやすい
いまはポアソン分布、裾の長いようになった時には
バリアンスを考え直す
・世界部分と西浦先生の共通部分と差
再生産方程式を解く
山中先生がアップしている→ロンドンのパッケージ
西浦先生:マニアック
感染者数を逆計算→劇的にダイナミクスをとらえるため
ドイツの
報告日別
アメリカ
発病日別
→政策を評価するため
ドイツ:報告日ベースだと、土日下がる(ウィークエンドバイアス)
・バイアスについて
年齢、地域、検査数
検査数:要請率の変動やっとでそう まだR(T)には組み込んでない
→見方には組み込んでいる
今できない:PCRのMAXのキャパシティーになってしまう
年齢:やっと流行曲線整備
・アメリカの議論の様子
日本:エキスパート1人という状況はあり得ない
→他に選択肢がない
勘所を抑えた人が増えると
・注文
実行再生産数:再現している〇
ほかのグループにも参入してほしい
オープンデータで実装できる!どんどんやりましょう!!
→とくに物理、情報の先生
モデル元年!
意外にシンプル!
推定したよあったら連絡してね!
・日本:分業はっきりしすぎている
FAXでやっていたのが報告が遅れる原因だった・・・
→結構、あったり;推測つく(変なノイズ)
・(アメリカの先生)よくわからない基準を作っている先生もいる
→なんでR(t)が使われているか
政策の評価ができる
なんで(細菌の先生の)基準が使われていないか考えてほしい
(西浦先生)まず、学術に出してみよう!!!
■締めのあいさつ