2月9日、
チョコボールに学ぶ実践的ベイズ統計モデリング入門
https://ml-for-experts.connpass.com/event/116830/
を聞いてきたのでメモメモ
なお、講義内容は、
チョコボール統計
http://chocolate-ball.hatenablog.com/
に載るらしい
目標
(1)統計モデリングとは何か
(2)ベイズ統計基礎
(3)Pythonを使ってやってみよう
対象:チョコボール
銀なら5枚、金なら1枚でおもちゃの缶詰がもらえる
→エンゼルの含有率
まれな現象の出現確率:頻度で計算すると、えらいことになる
あじぇんだ
・イントロダクション
・統計モデリングの目的
・最尤推定ハンズオン
・ベイズ推定ハンズオン
ソースコードは再編・再配布可能:クレジット入れてくれると
講師紹介
・チョコボールの秘密を解明するために、日々データを収集&解析
「チョコボール 統計」で検索
今日:ベイズ推定で銀のエンゼルの確率を・・・
統計モデリング
統計モデリングの目的
統計学入門 東京大学出版会 →入門だけど初学者は避けたほうがいい(入門詐欺)
統計学:データを収集し、組織化し、分析し、解釈する
統計モデリング:統計学の手法を使ってシステムを記述し、理解・説明するための枠組み
分布結果を活用するために、正規分布のような定式化されたモデルを仮定する
→定式化されたモデル
データ:正規分布と仮定(モデリング)
データに当てはめてパラメータを推定(μ、σ2を推定)
モデリング結果を評価し活用
「AI」と統計モデリング
AI:特定の技術ではなく、ある分野の技術の相称
学習と推論を行うためのソフトウェア
ニューラルネットワーク(NN)
・特徴空間に識別線を引く→データの分布を推定:統計モデリングとしての解釈
統計モデリングで得られること
・データの性質を理解できる
・活用の可能性
異常値、外れ値を定義
リスクを見積もった戦略を立てることができる
データが完全ではない時
→「
異端の統計学ベイズ」に書いてある
・楽しい
秘密を解明していく作業
なぜ確率分布を使ってモデリングするのか
・自然現象は本質的縫い不確定、計測には誤差が生じる
・コスト等の問題ですべての情報を使えない
統計モデリング
・データを当てはめてパラメータを推定
最尤推定
ベイズ推定
ハンズオンの流れ
・データ確認
・最尤法
・ベイズ推定
問題設定
・エンゼル出現確率の推定
・今回は銀のエンゼル
・キャンペーンでid=1のキャンペーンには銀のエンゼルは含まれない
モデル定義
370件のデータ→キャンペーン1をのぞいて327件
ベルヌーイ試行→二項分布
1回の施行で起こる確率がΘ、この試行をn回繰り返したときにエンゼルがK個当たる確率
→370回エンゼルかったら(n=370)17個当たった(k=17)
Θを変数とみなして、尤度関数を得る
→傾き0=微分を取って0
logとって微分する→計算すると、標本平均になる
何個買えば5個当たる?:負の2項分布を使う
→パラメータを入れ替えて式を作っている
→累積で考える
lossと尤度関数は同じ(どう定義して、何と呼ぶかの違い)
ベイズは何をやっているのか?
・20個買ってたまたま1個あたり→予測の信頼性
あいまいさを表現できる
分布で表現できる
・ベイズの定理
P(A|B)∝P(B|A)P(A) ぴー びー いーぶん えー ぴー えー
事前分布、尤度
。尤度は最尤推定のモデルと一緒
・事前分布はその問題に対しての知識を表現する
ベイズの定理 P(Θ|X)∝ P(X|Θ)P(Θ)
尤度関数 事前分布
事前分布:ベータ分布を設定(使いやすいからベータ分布のだけ)
ベータ関数 αとβでいろんなものが作れる
計算方法
今回は解析的に解けるけど
一般的には数値的なMCMCを使う
pymcを使う
モデルで箱を用意する
事前分布 β分布 α、β=1(一様分布)
尤度 二項分布
データ数が多ければ、事前分布では変わらない
データ数が少ない時に変わる
平均
ネガティブ予想
ポジティブ予想
→ができる(95%信頼区間)
背景を想像(仮説立案)しながらモデルを改良していく(仮説の検証)
チョコボールは面白い
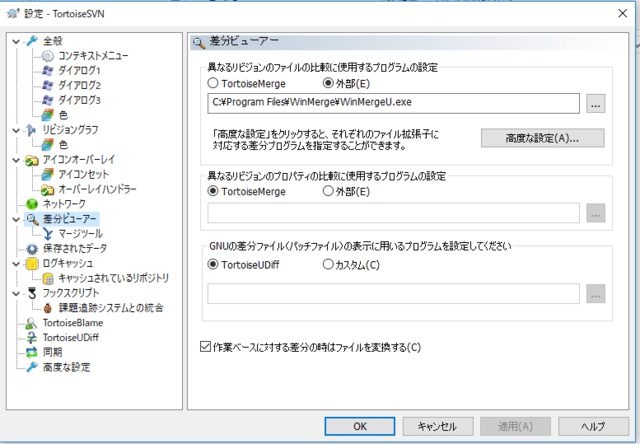
 WinMergeを先に入れて、TortoiseSVNを後で入れた際に、設定で、
WinMergeを先に入れて、TortoiseSVNを後で入れた際に、設定で、