この前のエントリ「バグの成長曲線(ソフトウェア信頼度成長モデル)の係数の意味」で、式の変数の意味がわかると、Excelで求められるって書いておきながら、肝心の求め方を書いていなかった!というので、今日は、バグの信頼度曲線(成長曲線)書いて、予測する方法を書きます。
■お題
あなたが、残念ながら情報学科とか、データを扱う学科を出てしまったとします。
上司は、当然のことのように、
今、バグの実績があるんだけど、
これを成長曲線って言うの、
S字曲線って言うのにあてはめて、
今後、どれくらいのバグがでるのか、
何時頃収束するのか、予測して欲しい
と、言ってきたとします。
実際には、大学では教えていないかもしれません
(たぶん、教えないと思う。このレベルだと、修士で教えるんじゃないかな?)
でも、「出来ません!」っていうと、
「おまえ、情報学科出てきたんだろうぶつくさぶつくさ・・・」
といって教えてくれません。
どうしたらいいんでしょう・・・
という状況
■概要
今回はExcelでやります(Rでも出来るけど、今回はExcel)。
まず、バグの実績に対して、信頼度曲線をあてはめないといけません。
当てはめるべき信頼度曲線は、
バグの成長曲線(ソフトウェア信頼度成長モデル)の係数の意味
http://blog.goo.ne.jp/xmldtp/e/5c5bb699055e3c376cf1cf61ece3e7d4
で書いた、指数形、遅延S字形、習熟S字型など。
で、その関数に対して、a,b,cの値を最小2乗法であてはめを行います。
このとき、Excelのソルバーを使います。
a,b,cが決まれば、あとは、日数を延ばしていけば、予測できますよね。
■準備1.ソルバーを入れる。
ソルバーを使います。Excelに入っているか、確認してください。
Excelを立ち上げて、「データ」に「ソルバー」って言うのがなければ、
入っていません。入れましょう。
入れ方は、
第九回 1分で完了! 便利なExcelアドイン「ソルバー」を追加しよう!
http://www.hello-pc.net/howto-excel/solver/
にありますが、うちのとは、バージョンが違ったので、うちの場合を披露します。
1.新規作成するようなときに出すボタンから、
下にある「Excelのオプション」をクリック
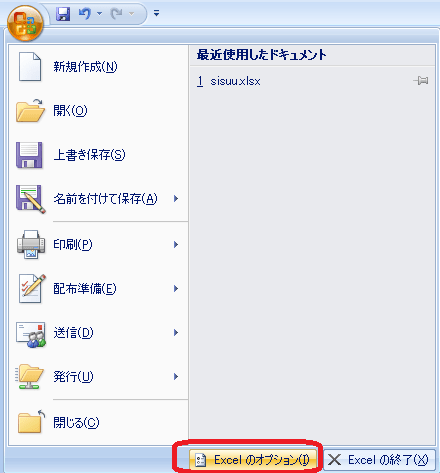
2.出てきたダイアログ
アドイン→ソルバーアドインを選択。下で「設定」ボタンをクリック
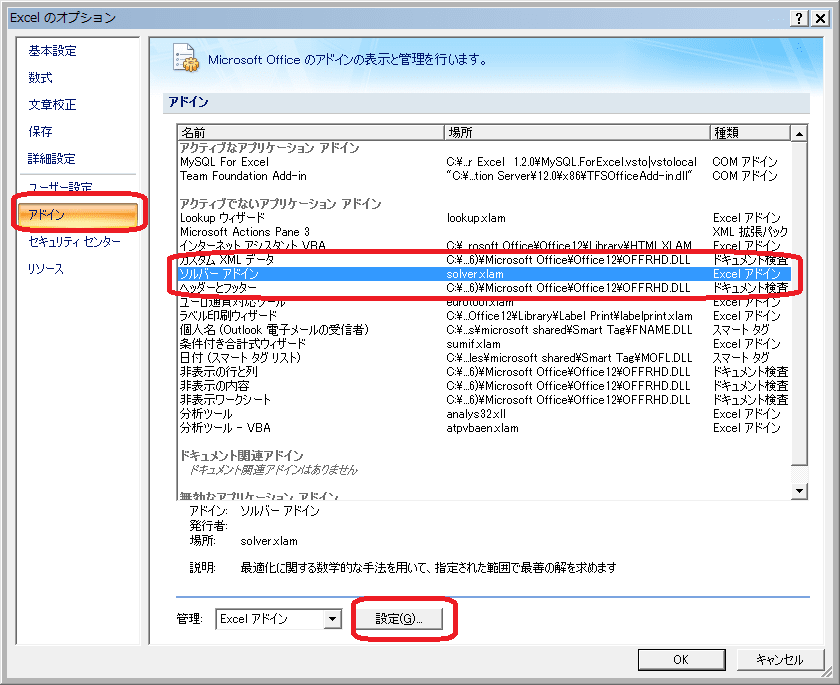
3.出てくるダイアログで「ソルバーアドイン」にチェックを入れて、OK
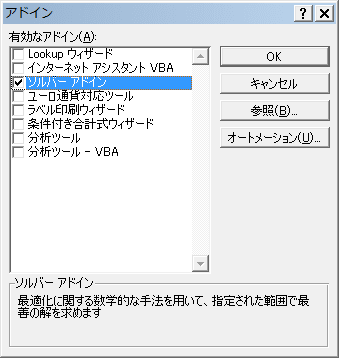
4.以下のダイアログが「出てきたら」、「はい」をクリックすると、インストール実行
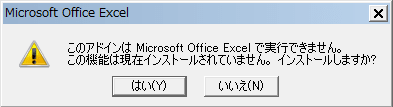
で、インストール完了
■準備2.データ入力
準備1は、1回やればいい。今度は、毎回行うこと。
曲線の元&予測する為のデータを入力します。
A列に、日数(または、時間数、週数)などを入力します
日にちではなく、開始日を0として、経過した日数(または、時間数、週数)
を書きます。
B列には、実際のバグの数を書きます(A列の日数に対応させて・・・ですよ)
A,B列は、本当はC,Dでも、F,GでもOKです。
でも、隣接している列のほうが、やりやすいはずです
以下、A列に日数、B列に実績値を入れたとして、話します。
■成長曲線の式をきめ、邪魔にならないところにa,b,cをおく
まず、今回あてはめを行う成長曲線の数式を決めます
例えば、指数形の場合式は、a(1-exp(-bt))です。
今回の例は、これにしましょう。
この中で、あてはめを行うのは、a,bです。
なので、a,bの値を、適当なところ(今回は後で示しますが、
aの値をセルB16に、bの値をセル17)におきます。
このとき、値はテキトーでいいです
(本当は多少考えますが、考え方は、失敗した後で説明するので
今回は適当に・・・)
■理論値と最小2乗の値をおく
C桁には、計算で求めた理論値を書きます。
今、式はa(1-exp(-bt))です。
そしてaはセルB16、bはセルB17にあるので、
●C列のはじめC3は、
=$B$16 * ( 1 - EXP( -1 * $B$17 * $A3 ) )
となります。
●D列は、実績値と理論値の差の2乗を求めます。
2乗を求めるから、最小2乗法です。
たとえば、D3だと、
=(B3-C3)^2
です。
●D列の一番最後で、最小2乗の合計値を求めます。
D3~D13まで埋めたとすると、D14で、
=sum(D3:D13)となります。
ここまで行うと、以下のようになります。
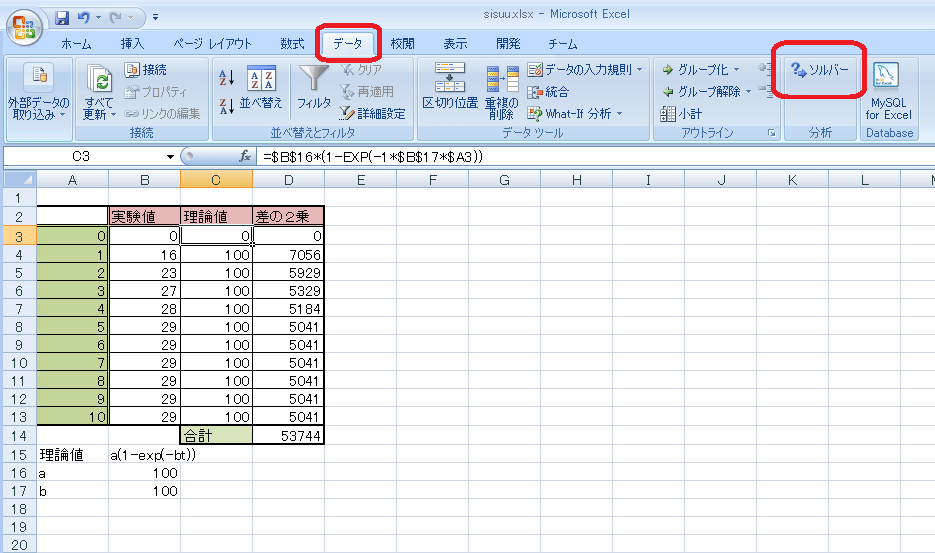
■ソルバーの起動
ここで、「データ」タブの「ソルバー」をクリック
(上図で赤く囲ったところ)
出てきたダイアログで、

「目的セル」は
最小2乗の合計値。今回はD14
「目標値」は
”最小2乗法”なので、最小値
「変化させるセル」は
a,bの値のセルのこと。B16とB17なので、
そのセルを囲むと、図のように出てくる
今回は制約条件はいれなくていい・・
ので、これで、「実行」ボタンを押して、実行!
■大失敗
そうして出てきた結果が、こちら!

a,bと理論値が変化している
理論値全部26.8って、
一直線やないか!
だめだめ、却下!
このように、テキトーにa,bを入れてしまうと、
そのあたりでよい答え(局所解)に陥ってしまう。
なので、ある程度まじめにa,bを決定しよう。
ちなみに、出てきたダイアログ「キャンセル」をクリックすると、
元の値に戻る
■a,bの値をきめる。
前に書いたとおり、aが収束値なので、収束しそうな値を書く
(はずれてもぜんぜんOK。テキトーに)
bですが、a(1-exp(-bt))なので、図の半分くらいのところに点を打ちたいなら、
1-exp(-bt)=1/2くらい。ここで、exp(-1)=1/2.7位なので、
実績値が真ん中ぐらいにあるときのtの値に対して、-bt=-1位にしたい。
いま、t=1のとき実績値が16で、ちょうどいいかんじなので、
-b*1=-1,b=1
って、ここまで考えるのがめんどくさかったら、テキトーでいいよ。
それがいやな人は、以下の手順で求める
・収束する前(できれば半分くらい)のtの値をもとめる
・そのtの逆数をbとする
こうしたのが、下の図
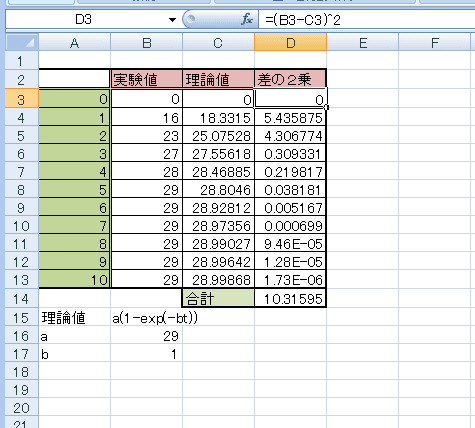
■グラフかいてみた
で、もう一回「実行」
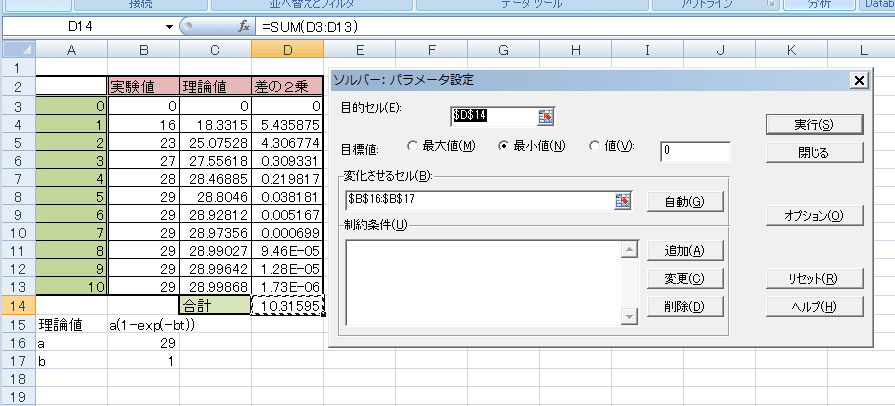
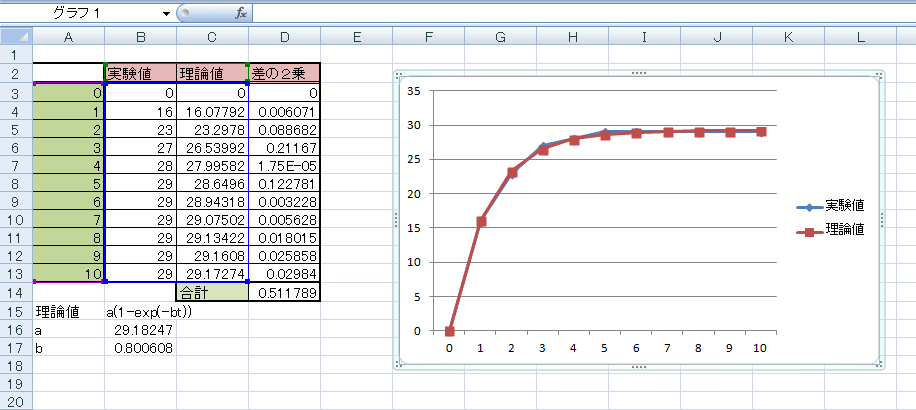
こんなんでてきました。「OK」で、この値が入る
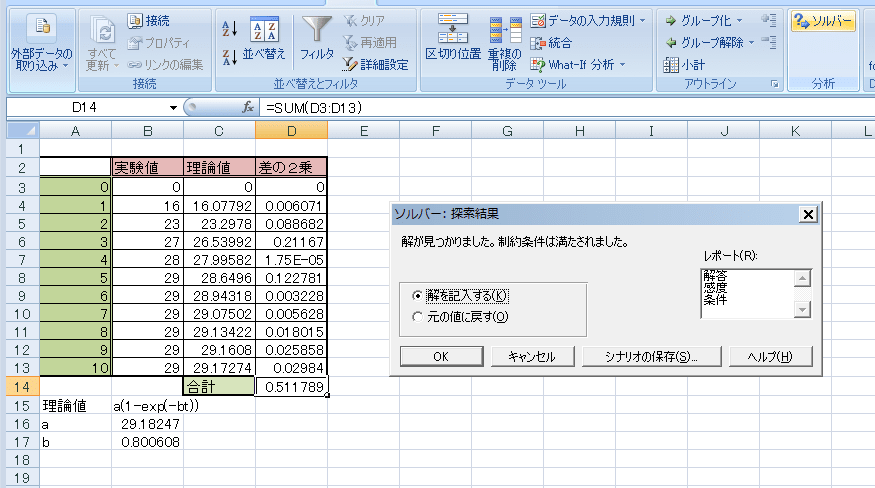
理論値と実績をグラフにして見ました
■予測する場合
A列をさらに下に伸ばし、
C列を下に伸ばす(フィルする)、ないしは、C列のどこかをコピー、下にペーストしていく
■式を変えたい場合
C列の式をかえる。習熟S字の場合、cがでてくるので、
B19にCの値をいれ、ソルバーのダイアログ、
「変化させるセル」を「$B$16:$B$19」に変える
■お題
あなたが、残念ながら情報学科とか、データを扱う学科を出てしまったとします。
上司は、当然のことのように、
今、バグの実績があるんだけど、
これを成長曲線って言うの、
S字曲線って言うのにあてはめて、
今後、どれくらいのバグがでるのか、
何時頃収束するのか、予測して欲しい
と、言ってきたとします。
実際には、大学では教えていないかもしれません
(たぶん、教えないと思う。このレベルだと、修士で教えるんじゃないかな?)
でも、「出来ません!」っていうと、
「おまえ、情報学科出てきたんだろうぶつくさぶつくさ・・・」
といって教えてくれません。
どうしたらいいんでしょう・・・
という状況
■概要
今回はExcelでやります(Rでも出来るけど、今回はExcel)。
まず、バグの実績に対して、信頼度曲線をあてはめないといけません。
当てはめるべき信頼度曲線は、
バグの成長曲線(ソフトウェア信頼度成長モデル)の係数の意味
http://blog.goo.ne.jp/xmldtp/e/5c5bb699055e3c376cf1cf61ece3e7d4
で書いた、指数形、遅延S字形、習熟S字型など。
で、その関数に対して、a,b,cの値を最小2乗法であてはめを行います。
このとき、Excelのソルバーを使います。
a,b,cが決まれば、あとは、日数を延ばしていけば、予測できますよね。
■準備1.ソルバーを入れる。
ソルバーを使います。Excelに入っているか、確認してください。
Excelを立ち上げて、「データ」に「ソルバー」って言うのがなければ、
入っていません。入れましょう。
入れ方は、
第九回 1分で完了! 便利なExcelアドイン「ソルバー」を追加しよう!
http://www.hello-pc.net/howto-excel/solver/
にありますが、うちのとは、バージョンが違ったので、うちの場合を披露します。
1.新規作成するようなときに出すボタンから、
下にある「Excelのオプション」をクリック

2.出てきたダイアログ
アドイン→ソルバーアドインを選択。下で「設定」ボタンをクリック

3.出てくるダイアログで「ソルバーアドイン」にチェックを入れて、OK

4.以下のダイアログが「出てきたら」、「はい」をクリックすると、インストール実行

で、インストール完了
■準備2.データ入力
準備1は、1回やればいい。今度は、毎回行うこと。
曲線の元&予測する為のデータを入力します。
A列に、日数(または、時間数、週数)などを入力します
日にちではなく、開始日を0として、経過した日数(または、時間数、週数)
を書きます。
B列には、実際のバグの数を書きます(A列の日数に対応させて・・・ですよ)
A,B列は、本当はC,Dでも、F,GでもOKです。
でも、隣接している列のほうが、やりやすいはずです
以下、A列に日数、B列に実績値を入れたとして、話します。
■成長曲線の式をきめ、邪魔にならないところにa,b,cをおく
まず、今回あてはめを行う成長曲線の数式を決めます
例えば、指数形の場合式は、a(1-exp(-bt))です。
今回の例は、これにしましょう。
この中で、あてはめを行うのは、a,bです。
なので、a,bの値を、適当なところ(今回は後で示しますが、
aの値をセルB16に、bの値をセル17)におきます。
このとき、値はテキトーでいいです
(本当は多少考えますが、考え方は、失敗した後で説明するので
今回は適当に・・・)
■理論値と最小2乗の値をおく
C桁には、計算で求めた理論値を書きます。
今、式はa(1-exp(-bt))です。
そしてaはセルB16、bはセルB17にあるので、
●C列のはじめC3は、
=$B$16 * ( 1 - EXP( -1 * $B$17 * $A3 ) )
となります。
●D列は、実績値と理論値の差の2乗を求めます。
2乗を求めるから、最小2乗法です。
たとえば、D3だと、
=(B3-C3)^2
です。
●D列の一番最後で、最小2乗の合計値を求めます。
D3~D13まで埋めたとすると、D14で、
=sum(D3:D13)となります。
ここまで行うと、以下のようになります。

■ソルバーの起動
ここで、「データ」タブの「ソルバー」をクリック
(上図で赤く囲ったところ)
出てきたダイアログで、

「目的セル」は
最小2乗の合計値。今回はD14
「目標値」は
”最小2乗法”なので、最小値
「変化させるセル」は
a,bの値のセルのこと。B16とB17なので、
そのセルを囲むと、図のように出てくる
今回は制約条件はいれなくていい・・
ので、これで、「実行」ボタンを押して、実行!
■大失敗
そうして出てきた結果が、こちら!

a,bと理論値が変化している
理論値全部26.8って、
一直線やないか!
だめだめ、却下!
このように、テキトーにa,bを入れてしまうと、
そのあたりでよい答え(局所解)に陥ってしまう。
なので、ある程度まじめにa,bを決定しよう。
ちなみに、出てきたダイアログ「キャンセル」をクリックすると、
元の値に戻る
■a,bの値をきめる。
前に書いたとおり、aが収束値なので、収束しそうな値を書く
(はずれてもぜんぜんOK。テキトーに)
bですが、a(1-exp(-bt))なので、図の半分くらいのところに点を打ちたいなら、
1-exp(-bt)=1/2くらい。ここで、exp(-1)=1/2.7位なので、
実績値が真ん中ぐらいにあるときのtの値に対して、-bt=-1位にしたい。
いま、t=1のとき実績値が16で、ちょうどいいかんじなので、
-b*1=-1,b=1
って、ここまで考えるのがめんどくさかったら、テキトーでいいよ。
それがいやな人は、以下の手順で求める
・収束する前(できれば半分くらい)のtの値をもとめる
・そのtの逆数をbとする
こうしたのが、下の図

■グラフかいてみた
で、もう一回「実行」

こんなんでてきました。「OK」で、この値が入る

理論値と実績をグラフにして見ました

■予測する場合
A列をさらに下に伸ばし、
C列を下に伸ばす(フィルする)、ないしは、C列のどこかをコピー、下にペーストしていく
■式を変えたい場合
C列の式をかえる。習熟S字の場合、cがでてくるので、
B19にCの値をいれ、ソルバーのダイアログ、
「変化させるセル」を「$B$16:$B$19」に変える


























