はじめに
前回の記事のコメント欄で、yamayositoさんから以下のような指摘を受けました。図1を例証しながら、以下のように論じておられます。
>勾配が1の直線部分は降雨量がそのまま流出量になる領域です。二つの直線部分の交点の降雨量が飽和雨量です。(中略)
>河川工学での定義にしたがう限り、「引き伸ばしの誤謬」はありません。森林水文学で損失高が飽和雨量であるとの定義にしたがう議論は、河川工学では採用されないでしょう。少なくとも貯留関数法で降雨から流量を計算する場合は、飽和雨量は河川工学の定義にしたがうべきです。
このご批判に答える形で、以下の三点を論じます。第一に河川工学における「飽和雨量」の定義がいかにおかしいか。第二に貯留関数法という流出解析モデルがいかに自然の現実から乖離しているのか。第三に国交省はいかに貯留関数法を用いて洪水流量の計算値を過大に算出しているのか。
「何やら難しそうだ」と思って敬遠しないで下さい。貯留関数法というモデルの欠陥を恣意的に悪用することにより、国交省は国民を騙し、八ツ場ダム建設を決めました。総額4600億円の事業です。全く必要のない事業のために、赤ん坊からお年寄りまで、国民一人当たり4600円もの支出を強いたのです。国交省は、審議会で偽証をし、「利根川の基本高水22000」という数値に疑問を呈した委員たちを騙し、4600億円もの血税を詐取したのです(ブログ「ダム日記2」のこの記事およびこの記事などを参照)。これを犯罪と呼ばずして、何をそう呼んだらよいのでしょうか? 国民一人一人が、こうしたトリックに騙されぬよう十分な懐疑精神を持たねばなりません。でなければ、彼らはそれに付け込んで、さらに私たちを騙そうとするでしょう。

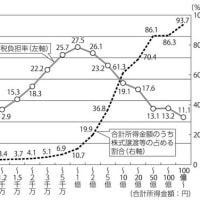
図1 国交省河川局の河川整備基本検討小委員会で提示された図
http://www.mlit.go.jp/river/shinngikai_blog/shaseishin/kasenbunkakai/shouiinkai/kihonhoushin/051206/pdf/s1.pdf
曲線であるべきものを直線で近似
図1のグラフを説明します。横軸に一連降雨の総雨量、縦軸に洪水時に河川に流出した総流出量を取ります。大小さまざまな降雨イベントの降雨量と洪水時の流出量を調べ、それをプロットすると上のグラフのようになります。
貯留関数法では、この散布図の関数による表現として、傾き0.5程度の直線と、傾き1.0の直線という二本の直線で近似します。そして、二本の直線の交点を「飽和雨量」としています。
しかしグラフの形状を見れば、読者の皆様は容易に気づくでしょう。このグラフは、本来曲線で近似すべきです。50mm以下の小規模な降雨では、降雨に対する流出量は、最初0.1から0.2くらい。しかしグラフの傾きは次第に0.3、0.5、0.7、0.9と上昇していき、最終的に漸近線である傾き1の直線に近づいていきます。このような形状は、本来的に曲線で近似すべきものです。
ちなみに、国交省が定義した直線のグラフの傾きを「流出係数」と呼びます。利根川の場合、国土交通省は、累加雨量48mmまでを傾き0.5で計算し、48mmで土壌は飽和して(=飽和雨量)、その後、降った雨はすべて流出する、つまり傾きは1になると仮定して流出計算を行っていました。48mmの飽和雨量に達するまでは0.5(つまり50%)が流出し、48mmを超えた直後きから1.0(つまり100%)が流出するという二段階モデルです。
飽和雨量を二本の直線の交点とする考えは、貯留関数法のモデル上の要請から成されたものです。自然界の現実には合致しません。本来は曲線であるものを、モデルで計算しやすいように二本の直線で近似したにすぎないのです。現実の自然界は、飽和点の前は0.5で、飽和点を超えるといきなり1になるというように、単純でデジタルな変化はしません。
「二本の直線」の交点とする考えでは、片方の直線の位置を決める際、どの雨量のプロットまでを含めるかで、飽和雨量の値を上げたり下げたり操作することが可能になります。実際、国交省は図1においても、本来100mm以上であるべき飽和雨量の値を、直線の位置を操作することにより何とか100mm以下に見せかけようと苦心しております。
本来、飽和雨量の値はあくまでも、土壌が何mmの降雨を貯留し得るのかで定義すべきです。故に、土壌の物理学的組成の解析から決定されるべきです。いくらでも操作可能な「二本の直線」の交点などで決めてよいわけがないのです。
「飽和雨量」を過少に設定すると計算流量は過大になる
国土交通省は利根川水系において、本来は100mm以上の値を当てはめるべきところの飽和雨量の値を、48mmで計算しておりました。図2を見てください。実際の自然では、100mmを超えたあたりで傾きが1に近くなる曲線を描くにも関わらず、国交省は48mmで折れ曲がって、それ以降は1になるというモデルで計算していたのです。国交省の計算モデルの前提は、図に示した赤い折れ線です。実際の自然は下に示した黒い曲線になります。赤い線と黒い線の差が、国交省が過大に計算した計算流量ということになります。
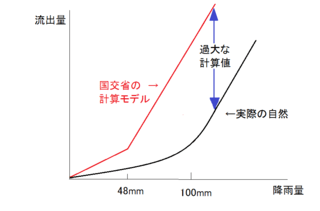
図2 飽和雨量を過少に設定すると計算値は過大になる
縦軸の値は、洪水時の増水の初めから終わりまでの総流出量を示します。国交省の定義する「基本高水」とは、瞬間最大のピーク時の流出量(=ピーク流量)のことです。瞬間最大ピーク流量と総流出量は違いますので注意が必要です。図2で示された過大な値イコール基本高水の過大な計算値というわけではありません。計算上のピーク流量は、後に述べるように、降雨波形の場合によっては、総流出量以上に過大に算出されます。たとえば、総流出量が1.3倍に過大に計算されれば、ピーク流量は1.6倍に過大に算出されるという具合です。
貯留関数法における、0.5からいきなり1.0へ飛躍するという二段階モデルの大ざっぱな仮定に従うと、とくに中規模降雨から得られたパラメータを大規模降雨に当てはめようとすればするほど、数値積分の際の誤差が積み重なって、計算誤差が広がっていきます。計算精度を高くしようとすれば、降雨の降り始めの初期段階では0.2程度しか流出せず、それが0.3、0.5、0.7・・・と段階的に増えていき、降雨が大きくなるにつれて1.0に近づいていくというモデルにせねばなりません。少しづつ流出率が上昇していくという多段階モデルにすれば、計算精度は改善されます。しかし国交省は、過去に観測事例のない大規模降雨に対し二段階モデルを当てはめているのです。
ちなみに、1947年のカスリーン洪水では、実際に流れた実測値は16000m3/秒程度と推定されているのに対し(ただし国交省は17000m3/秒と推定)、国交省が貯留関数法で計算したとされる計算値が22000m3/秒ですから、計算ピーク流量は実測ピーク流量の1.375倍に高くなっています。
コンクリートタンクの誤謬
貯留関数法の仕組みをもう少し詳しく説明します。図3、図4を見て下さい。貯留関数法は、流出域を一つの巨大なタンクになぞらえてモデル化します。
タンクの貯留量(S)と河川への流出量(Q)のあいだには、
S=KQ^P ・・・・・ (1)
という関係が仮定されています(単なるモデル上の仮定で現実ではないことに注意)。ここでKとPは流域ごとに決まる定数です。
降雨量(R)と流出量(Q)と貯留量(S)の間には
R-Q = dS / dt ・・・・・ (2)
という関係があります。(2)式は、流入から流出を引いたものが貯留量の変化率になるという貯留量の定義を示したものですから、方程式ではなく定義式です。
これら(1)式と(2)式から得られる微分方程式を、数値積分することによって計算し、河川の流出量を求めていくのが貯留関数法のエッセンスです。

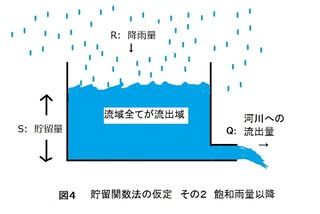
ただし、流出の仕方は、土壌の飽和以前と飽和以降で異なると仮定されています。図3が飽和前のモデルで、図4が飽和後のモデルです。ここで導入されるのが「一次流出率(f)」と「飽和雨量(Rsa)」という、森林の状態に深く関係する二つのパラメータです。
貯留関数法では、累加降雨量が飽和雨量に達する以前は、タンクを「流出域」と「浸透域」という二つの異なる漕に分けてモデル化します。浸透域に降った雨は、河川に流出することなく、土壌を鉛直下方に移動して、地下に浸透すると仮定されています。浸透域のタンクに水は溜まらないという仮定です(すべてモデルを構築するための仮定です。実際の自然の姿ではありません。念のため)。
土壌が飽和するまでは、浸透域に降った雨は河川に流出しないと仮定されています。浸透域を通って地下に浸透した水は、洪水が終わってからゆっくりと河川に流出してくる「基底流量」になります。晴天でも川に流れている水が「基底流量」です。森林土壌は雨水の浸透能力が高いので、流域の森林面積が大きく、また森林土壌が発達するほど、浸透域の面積は大きくなります。
流出の初期段階で、流出域が全流域面積の何%の面積を占めるのかを示すのが、一次流出率(f)というパラメータです。森林土壌が発達し、浸透域が大きいほど、一次流出率は小さくなります。
利根川では、一次流出率が0.5(つまり50%)と仮定されています。この仮定は、ちょうど流域面積の大きさのタンクを二つに分け、50%が流出域で、残りの50%が浸透域であるという仮定です。つまり降った降雨の50%しか河川には流出しないことになります。
ついで貯留関数法では、累加雨量が「飽和雨量」を超えた途端、浸透域は消滅するという仮定が置かれています。図3のようだった流出モデルは、飽和雨量を超えると図4のようなモデルに変化します。この二段階モデルが貯留関数法の特徴です。
森林土壌が発達すればするほど、多くの雨水を貯留可能ですので、飽和雨量の値は大きくなります。
飽和雨量を超えると、モデルの形は変わります。図3から図4のモデルに変化します。浸透域で仮定されていた地下への浸透孔は閉鎖され、あたかもタンクはコンクリートで覆われてしまったかのように、河川に流出する以外は全く地下には浸透しないというモデルになります。そして降った雨は、すべて①と②で示された方程式に従って、河川に流出するようになるのです。
賢明な読者の皆様の中には、既に気づいている方も多いと思います。このモデルは自然界の現実からとんでもなく乖離しています。どこが非常識なのでしょうか?
「飽和雨量を超えるとタンクから鉛直下方へと水が一滴も漏れない」という仮定が非常識なのです。私はこれを「コンクリートタンクの誤謬」と呼びたいと思います。実際の自然界のタンクは、隙間だらけで、飽和雨量以降も雨水をどんどん地下に浸透させているのに、貯留関数法のモデル上のタンクは、あたかもコンクリートで覆われているが如く、水を一滴も地下に浸透させないのです。このコンクリートタンクの誤謬により、ある降雨パターンの際には、計算流量はとくに過大に算出されることになります。

東京高裁に出した意見書に掲載した図
出所: http://www.yamba.jpn.org/shiryo/tokyo_k/tokyo_k_g_iken_seki_2.pdf
貯留関数法で二山型洪水はうまく計算できない
ここでもう一度、利根川における昭和33(1958)年と昭和34(1959)年の利根川の流量の実測値と計算値のグラフを見てください。前回の記事でも引用したのと同じ図です。昭和34年洪水は、雨の降り方が二山型になっています。そのため河川流量も、最初のピークの後に一度下がり、次いで二番目のピークが発生するという「二山型洪水」になります。
貯留関数法では、一山型洪水に適合したパラメータを用いると二山型洪水をうまく計算できないという欠点が知られています。この欠陥をうまく利用すると、基本高水の過大算出が可能になります。1947年のカスリーン洪水は典型的な二山型洪水でした。二山洪水で計算値が過大になるのは、「コンクリートタンクの誤謬」に起因する部分が大きいのです。
実際、1958(昭和33)年の一山洪水には当てはまった48mmモデルによって、森林状態にほとんど変化ないであろう翌昭和34年の二山洪水を計算すると、計算値は実測値よりも10%過大な値になります。前回の記事で解説した「引き伸ばしの誤謬」に加え、「コンクリートタンクの誤謬」も、計算値の過大算出に寄与しています。
激しい雨のあとに小降りになり、再び豪雨になるという二山型洪水では、最初の雨のピークの際にモデル上で仮定されたコンクリートタンクは飽和すると仮定されます。二番目の雨のピークが来た際には、タンクは満杯なので、すべての降雨が河川に流出すると、モデル上では計算されます。
しかし実際の自然はどうでしょう。最初の雨によってたしかに土壌に雨水が溜まります。しかし、二番目のピークがくるまでの小降りのあいだに、地下に雨水がどんどん浸透していますから、タンクには再び空き容量が発生します。二番目の豪雨がくるまでに、森林土壌の雨水浸透能力はある程度回復しているのです。
貯留関数法のモデル上では、タンクはコンクリートですから、「空き容量」は存在しないことになります。その結果、いったん小降りになった雨が再び勢いを増すという二山目には、モデル上の浸透域が存在せず、計算ピーク流量は実際よりも過大になるのです。
1959(昭和34)年洪水のグラフをよく見てみましょう。実測値のグラフは、一山目の後の小降りの時に流出量は小さくなっています。雨が浸透して、森林土壌に空き容量が発生しているからと思われます。これが現実の自然です。しかし貯留関数法のモデル上では、コンクリートタンクで覆われているため、飽和雨量以降の降雨は浸透しません。その結果、一山目の後でも河川流出量は十分に下がらず、そこに二山目のピークがやってくるので、計算値は実際よりも過大に跳ね上がってしまいます。
馬淵大臣の国会答弁にあった通り、昭和34年洪水では、飽和雨量を65mmに設定しないとうまく実測値に適合しません。コンクリートのタンクで覆われているという仮定をカバーする分だけ、飽和雨量をあらかじめ高めに設定せねば、実測値には適合しないことになります。
「200年に1度」といわれるカスリーン台風の際の318mmの大規模降雨は、昭和34年のような「二山型洪水」を、さらに規模を大きくしたものです。よって貯留関数法によるカスリーン洪水の計算流量は、さらに過大に算出されるのです。
前回の記事のコメント欄で、yamayositoさんから以下のような指摘を受けました。図1を例証しながら、以下のように論じておられます。
>勾配が1の直線部分は降雨量がそのまま流出量になる領域です。二つの直線部分の交点の降雨量が飽和雨量です。(中略)
>河川工学での定義にしたがう限り、「引き伸ばしの誤謬」はありません。森林水文学で損失高が飽和雨量であるとの定義にしたがう議論は、河川工学では採用されないでしょう。少なくとも貯留関数法で降雨から流量を計算する場合は、飽和雨量は河川工学の定義にしたがうべきです。
このご批判に答える形で、以下の三点を論じます。第一に河川工学における「飽和雨量」の定義がいかにおかしいか。第二に貯留関数法という流出解析モデルがいかに自然の現実から乖離しているのか。第三に国交省はいかに貯留関数法を用いて洪水流量の計算値を過大に算出しているのか。
「何やら難しそうだ」と思って敬遠しないで下さい。貯留関数法というモデルの欠陥を恣意的に悪用することにより、国交省は国民を騙し、八ツ場ダム建設を決めました。総額4600億円の事業です。全く必要のない事業のために、赤ん坊からお年寄りまで、国民一人当たり4600円もの支出を強いたのです。国交省は、審議会で偽証をし、「利根川の基本高水22000」という数値に疑問を呈した委員たちを騙し、4600億円もの血税を詐取したのです(ブログ「ダム日記2」のこの記事およびこの記事などを参照)。これを犯罪と呼ばずして、何をそう呼んだらよいのでしょうか? 国民一人一人が、こうしたトリックに騙されぬよう十分な懐疑精神を持たねばなりません。でなければ、彼らはそれに付け込んで、さらに私たちを騙そうとするでしょう。

図1 国交省河川局の河川整備基本検討小委員会で提示された図
http://www.mlit.go.jp/river/shinngikai_blog/shaseishin/kasenbunkakai/shouiinkai/kihonhoushin/051206/pdf/s1.pdf
曲線であるべきものを直線で近似
図1のグラフを説明します。横軸に一連降雨の総雨量、縦軸に洪水時に河川に流出した総流出量を取ります。大小さまざまな降雨イベントの降雨量と洪水時の流出量を調べ、それをプロットすると上のグラフのようになります。
貯留関数法では、この散布図の関数による表現として、傾き0.5程度の直線と、傾き1.0の直線という二本の直線で近似します。そして、二本の直線の交点を「飽和雨量」としています。
しかしグラフの形状を見れば、読者の皆様は容易に気づくでしょう。このグラフは、本来曲線で近似すべきです。50mm以下の小規模な降雨では、降雨に対する流出量は、最初0.1から0.2くらい。しかしグラフの傾きは次第に0.3、0.5、0.7、0.9と上昇していき、最終的に漸近線である傾き1の直線に近づいていきます。このような形状は、本来的に曲線で近似すべきものです。
ちなみに、国交省が定義した直線のグラフの傾きを「流出係数」と呼びます。利根川の場合、国土交通省は、累加雨量48mmまでを傾き0.5で計算し、48mmで土壌は飽和して(=飽和雨量)、その後、降った雨はすべて流出する、つまり傾きは1になると仮定して流出計算を行っていました。48mmの飽和雨量に達するまでは0.5(つまり50%)が流出し、48mmを超えた直後きから1.0(つまり100%)が流出するという二段階モデルです。
飽和雨量を二本の直線の交点とする考えは、貯留関数法のモデル上の要請から成されたものです。自然界の現実には合致しません。本来は曲線であるものを、モデルで計算しやすいように二本の直線で近似したにすぎないのです。現実の自然界は、飽和点の前は0.5で、飽和点を超えるといきなり1になるというように、単純でデジタルな変化はしません。
「二本の直線」の交点とする考えでは、片方の直線の位置を決める際、どの雨量のプロットまでを含めるかで、飽和雨量の値を上げたり下げたり操作することが可能になります。実際、国交省は図1においても、本来100mm以上であるべき飽和雨量の値を、直線の位置を操作することにより何とか100mm以下に見せかけようと苦心しております。
本来、飽和雨量の値はあくまでも、土壌が何mmの降雨を貯留し得るのかで定義すべきです。故に、土壌の物理学的組成の解析から決定されるべきです。いくらでも操作可能な「二本の直線」の交点などで決めてよいわけがないのです。
「飽和雨量」を過少に設定すると計算流量は過大になる
国土交通省は利根川水系において、本来は100mm以上の値を当てはめるべきところの飽和雨量の値を、48mmで計算しておりました。図2を見てください。実際の自然では、100mmを超えたあたりで傾きが1に近くなる曲線を描くにも関わらず、国交省は48mmで折れ曲がって、それ以降は1になるというモデルで計算していたのです。国交省の計算モデルの前提は、図に示した赤い折れ線です。実際の自然は下に示した黒い曲線になります。赤い線と黒い線の差が、国交省が過大に計算した計算流量ということになります。

図2 飽和雨量を過少に設定すると計算値は過大になる
縦軸の値は、洪水時の増水の初めから終わりまでの総流出量を示します。国交省の定義する「基本高水」とは、瞬間最大のピーク時の流出量(=ピーク流量)のことです。瞬間最大ピーク流量と総流出量は違いますので注意が必要です。図2で示された過大な値イコール基本高水の過大な計算値というわけではありません。計算上のピーク流量は、後に述べるように、降雨波形の場合によっては、総流出量以上に過大に算出されます。たとえば、総流出量が1.3倍に過大に計算されれば、ピーク流量は1.6倍に過大に算出されるという具合です。
貯留関数法における、0.5からいきなり1.0へ飛躍するという二段階モデルの大ざっぱな仮定に従うと、とくに中規模降雨から得られたパラメータを大規模降雨に当てはめようとすればするほど、数値積分の際の誤差が積み重なって、計算誤差が広がっていきます。計算精度を高くしようとすれば、降雨の降り始めの初期段階では0.2程度しか流出せず、それが0.3、0.5、0.7・・・と段階的に増えていき、降雨が大きくなるにつれて1.0に近づいていくというモデルにせねばなりません。少しづつ流出率が上昇していくという多段階モデルにすれば、計算精度は改善されます。しかし国交省は、過去に観測事例のない大規模降雨に対し二段階モデルを当てはめているのです。
ちなみに、1947年のカスリーン洪水では、実際に流れた実測値は16000m3/秒程度と推定されているのに対し(ただし国交省は17000m3/秒と推定)、国交省が貯留関数法で計算したとされる計算値が22000m3/秒ですから、計算ピーク流量は実測ピーク流量の1.375倍に高くなっています。
コンクリートタンクの誤謬
貯留関数法の仕組みをもう少し詳しく説明します。図3、図4を見て下さい。貯留関数法は、流出域を一つの巨大なタンクになぞらえてモデル化します。
タンクの貯留量(S)と河川への流出量(Q)のあいだには、
S=KQ^P ・・・・・ (1)
という関係が仮定されています(単なるモデル上の仮定で現実ではないことに注意)。ここでKとPは流域ごとに決まる定数です。
降雨量(R)と流出量(Q)と貯留量(S)の間には
R-Q = dS / dt ・・・・・ (2)
という関係があります。(2)式は、流入から流出を引いたものが貯留量の変化率になるという貯留量の定義を示したものですから、方程式ではなく定義式です。
これら(1)式と(2)式から得られる微分方程式を、数値積分することによって計算し、河川の流出量を求めていくのが貯留関数法のエッセンスです。


ただし、流出の仕方は、土壌の飽和以前と飽和以降で異なると仮定されています。図3が飽和前のモデルで、図4が飽和後のモデルです。ここで導入されるのが「一次流出率(f)」と「飽和雨量(Rsa)」という、森林の状態に深く関係する二つのパラメータです。
貯留関数法では、累加降雨量が飽和雨量に達する以前は、タンクを「流出域」と「浸透域」という二つの異なる漕に分けてモデル化します。浸透域に降った雨は、河川に流出することなく、土壌を鉛直下方に移動して、地下に浸透すると仮定されています。浸透域のタンクに水は溜まらないという仮定です(すべてモデルを構築するための仮定です。実際の自然の姿ではありません。念のため)。
土壌が飽和するまでは、浸透域に降った雨は河川に流出しないと仮定されています。浸透域を通って地下に浸透した水は、洪水が終わってからゆっくりと河川に流出してくる「基底流量」になります。晴天でも川に流れている水が「基底流量」です。森林土壌は雨水の浸透能力が高いので、流域の森林面積が大きく、また森林土壌が発達するほど、浸透域の面積は大きくなります。
流出の初期段階で、流出域が全流域面積の何%の面積を占めるのかを示すのが、一次流出率(f)というパラメータです。森林土壌が発達し、浸透域が大きいほど、一次流出率は小さくなります。
利根川では、一次流出率が0.5(つまり50%)と仮定されています。この仮定は、ちょうど流域面積の大きさのタンクを二つに分け、50%が流出域で、残りの50%が浸透域であるという仮定です。つまり降った降雨の50%しか河川には流出しないことになります。
ついで貯留関数法では、累加雨量が「飽和雨量」を超えた途端、浸透域は消滅するという仮定が置かれています。図3のようだった流出モデルは、飽和雨量を超えると図4のようなモデルに変化します。この二段階モデルが貯留関数法の特徴です。
森林土壌が発達すればするほど、多くの雨水を貯留可能ですので、飽和雨量の値は大きくなります。
飽和雨量を超えると、モデルの形は変わります。図3から図4のモデルに変化します。浸透域で仮定されていた地下への浸透孔は閉鎖され、あたかもタンクはコンクリートで覆われてしまったかのように、河川に流出する以外は全く地下には浸透しないというモデルになります。そして降った雨は、すべて①と②で示された方程式に従って、河川に流出するようになるのです。
賢明な読者の皆様の中には、既に気づいている方も多いと思います。このモデルは自然界の現実からとんでもなく乖離しています。どこが非常識なのでしょうか?
「飽和雨量を超えるとタンクから鉛直下方へと水が一滴も漏れない」という仮定が非常識なのです。私はこれを「コンクリートタンクの誤謬」と呼びたいと思います。実際の自然界のタンクは、隙間だらけで、飽和雨量以降も雨水をどんどん地下に浸透させているのに、貯留関数法のモデル上のタンクは、あたかもコンクリートで覆われているが如く、水を一滴も地下に浸透させないのです。このコンクリートタンクの誤謬により、ある降雨パターンの際には、計算流量はとくに過大に算出されることになります。

東京高裁に出した意見書に掲載した図
出所: http://www.yamba.jpn.org/shiryo/tokyo_k/tokyo_k_g_iken_seki_2.pdf
貯留関数法で二山型洪水はうまく計算できない
ここでもう一度、利根川における昭和33(1958)年と昭和34(1959)年の利根川の流量の実測値と計算値のグラフを見てください。前回の記事でも引用したのと同じ図です。昭和34年洪水は、雨の降り方が二山型になっています。そのため河川流量も、最初のピークの後に一度下がり、次いで二番目のピークが発生するという「二山型洪水」になります。
貯留関数法では、一山型洪水に適合したパラメータを用いると二山型洪水をうまく計算できないという欠点が知られています。この欠陥をうまく利用すると、基本高水の過大算出が可能になります。1947年のカスリーン洪水は典型的な二山型洪水でした。二山洪水で計算値が過大になるのは、「コンクリートタンクの誤謬」に起因する部分が大きいのです。
実際、1958(昭和33)年の一山洪水には当てはまった48mmモデルによって、森林状態にほとんど変化ないであろう翌昭和34年の二山洪水を計算すると、計算値は実測値よりも10%過大な値になります。前回の記事で解説した「引き伸ばしの誤謬」に加え、「コンクリートタンクの誤謬」も、計算値の過大算出に寄与しています。
激しい雨のあとに小降りになり、再び豪雨になるという二山型洪水では、最初の雨のピークの際にモデル上で仮定されたコンクリートタンクは飽和すると仮定されます。二番目の雨のピークが来た際には、タンクは満杯なので、すべての降雨が河川に流出すると、モデル上では計算されます。
しかし実際の自然はどうでしょう。最初の雨によってたしかに土壌に雨水が溜まります。しかし、二番目のピークがくるまでの小降りのあいだに、地下に雨水がどんどん浸透していますから、タンクには再び空き容量が発生します。二番目の豪雨がくるまでに、森林土壌の雨水浸透能力はある程度回復しているのです。
貯留関数法のモデル上では、タンクはコンクリートですから、「空き容量」は存在しないことになります。その結果、いったん小降りになった雨が再び勢いを増すという二山目には、モデル上の浸透域が存在せず、計算ピーク流量は実際よりも過大になるのです。
1959(昭和34)年洪水のグラフをよく見てみましょう。実測値のグラフは、一山目の後の小降りの時に流出量は小さくなっています。雨が浸透して、森林土壌に空き容量が発生しているからと思われます。これが現実の自然です。しかし貯留関数法のモデル上では、コンクリートタンクで覆われているため、飽和雨量以降の降雨は浸透しません。その結果、一山目の後でも河川流出量は十分に下がらず、そこに二山目のピークがやってくるので、計算値は実際よりも過大に跳ね上がってしまいます。
馬淵大臣の国会答弁にあった通り、昭和34年洪水では、飽和雨量を65mmに設定しないとうまく実測値に適合しません。コンクリートのタンクで覆われているという仮定をカバーする分だけ、飽和雨量をあらかじめ高めに設定せねば、実測値には適合しないことになります。
「200年に1度」といわれるカスリーン台風の際の318mmの大規模降雨は、昭和34年のような「二山型洪水」を、さらに規模を大きくしたものです。よって貯留関数法によるカスリーン洪水の計算流量は、さらに過大に算出されるのです。

















河川工学の飽和雨量の定義によれば、降雨量が多くなると飽和雨量が増加するとは言えないことはご理解いただけたようです。河川工学での飽和雨量の定義がおかしいと言われる件については、私も河川工学専攻でありませんので詳しくは論じられません。しかし降雨量と流出高の散布図を二本の直線で表現するのは最低限の近似であると理解しています。貯留関数法でも三本の直線で表現するやり方もありますし、分布型モデルでも3ステージで表現しています。所詮近似せざるを得ないことがあるのは認めざるを得ません。貯留関数法がいかに自然の現象から乖離しているかについても、残念ながら議論するは技術的背景を持ちません。マルチタンクモデルがよいとか、分布型モデルが最善であるとかの話を聞きますが、最終的にはどのような流出解析を実施しようと、国交省の「基準」にしたがう限り、最後には複数のピーク流量からどのピーク流量を基本高水流量に決定するかの問題が残ります。この問題に関係して治水安全度に見合う基本高水流量が過大になることが多いのです。すなわち貯留関数法で流出解析を実施する場合に、如何に最近の洪水に適用できる正確な平均的飽和雨量を求めたとしても、最終的にはピーク流量群からの選択問題が残るのです。
そして現在の「基準」では、計画雨量(利根川の場合は319mm/3日)まで引き伸ばされた対象降雨から時間的・地域的に発生しがたいと判断された対象降雨は棄却され、残った対象降雨からのピーク流量群の最大値を基本高水流量に決定し、その治水安全度は雨量確率と同じ(利根川の場合は1/200)であるとしています。このように決定された基本高水流量は治水安全度から見て過大になってしまうことが多いのです。引き伸ばされた対象降雨群が実際に計画規模の雨量確率で発生する降雨群を上手く代表しているか否かは全くの偶然で決まります。上手く代表している場合は、ピーク流量群の確率分布と実際の洪水のピーク流量群の確率分布との間のバイアスが小さくなり、その場合にはピーク流量群の最大値を基本高水流量に決定し、その治水安全度は雨量確率に同じであるとすると過大になります。バイアスが大きい場合、それほど過大にはなりません。このバイアスを小さくしようとするなら、対象降雨の数を増やすしか方法はありません。
利根川の場合は、総合確率法を採用し対象降雨も31ケと多く棄却もしていないので、過大になる要素はないのですが、雨量確率1/200に見合うピーク流量群の平均値21200m3/sの治水安全度を雨量確率と同じ1/200であるとしている点が間違っています。「改訂新版 建設省河川砂防技術基準(案) 同解説 調査編」の64ページに記載の確率年の計算式を適用したら、そのように判断せざるを得ないのです。確率年の計算式は大学の工学部学部学生用の教科書にも採用されています。
今問題になっている、貯留関数法で利根川の雨量から流量を計算する際の飽和雨量を48mmより適切と思われる飽和雨量、たとえば100mm、にしてカスリーン台風の降雨量と降雨波形でピーク流量を求めてもその治水安全度は1/200でないことをご理解下さい。現在の雨量から基本高水流量を求める方法では最終的にピーク流量群からの選択があり、その際に治水安全度が決まることがなかなか理解されないのです。
関先生が国交省は如何に貯留関数法を用いて洪水流量の計算値を過大に算出しているのかの持論の一つの根拠である「貯留関数法で二山型洪水はうまく計算できない」は、不勉強で初めて聞きます。それだから飽和雨量が48mmであることと相まって、「カスリーン台風の洪水の計算流量は、さらに過大に算出されるのです。」はそのまま受け取るとしても、見直された飽和雨量を採用してカスリーン台風の降雨量と降雨波形で計算したピーク流量が治水安全度1/200であるとの誤解は早く解くことが望ましいと考えます。また二山型洪水でなくとも、ピーク流量群の最大値を基本高水流量に決定し、その治水安全度を雨量確率に同じであるとすれば、過大なピーク流量になるのです。
過大な基本高水流量が決定される原因として、先ず現在の「基準」でピーク流量群の最大値を基本高水流量に決定し、その治水安全度を雨量確率と同じであると考えること、総合確率法のピーク流量の平均値の治水安全度を雨量確率と同じであると考えることがあり、次いで飽和雨量が小さいこと(最近のデータで見直す必要は大いにある)があげられると考えています。貯留関数法では二山型洪水はうまく計算できないことはその次に考えることではないかと思います。
治水安全度は流量の確率に基づくべきである。雨量が大きいほど流量が大きいとは限らないので、同じ事例をとっても雨量の確率と流量の確率とは一致しない。
流量の確率を求めるのに、流量の観測値だけで不足の場合は、多数の降雨事例について流量を計算して確率分布を求めるべきだ。
治水安全度は雨量確率でなく流量確率によるべきはおっしゃる通りです。同じ雨量でも降雨波形によって異なる流量を与えることから明らかです。
現実的に流量確率が求められるだけの年最大流量が蓄積された河川は少ないのです。特に中小河川においてはしかりです。
したがって「河川砂防技術基準」にしたがって雨量から流出計算し、基本高水流量を決定する方法を採用せざるを得ないのですが、得られたピーク流量群について統計的な取り扱いをしていないので、治水安全度に見合う基本高水流量が過大になりがちです。統計的な取り扱いは、「改訂新版 建設省河川砂防技術基準(案) 同解説 調査編」の64頁に確率年の計算式として記載されています。大学の教科書(例えばエース水文学 朝倉書店)などにも紹介されていて学問的にも認知されているはずです。
流量確率を求める際に欠測値があると、年最大流雨量から年最大流量を求めてその再現流量を採用することがあります。同様にある期間における年最大雨量から年最大流量を計算し、その再現流量から流量確率を求め方法も有用です。
私は長野市の浅川の治水安全度に見合う基本高水流量の決定で、ピーク流量群に確率年の計算式を適用し、得られた基本高水流量を30年間の年最大雨量からの再現流量より求めた流量確率で検証しています。
確率年の計算式を利根川に適用すると、総合確率法での雨量確率1/200に見合うピーク流量群の平均値21200m3/sの治水安全度は1/200でなく1/400になりますから、治水安全度1/200の基本高水流量は21200m3/sを1.16(流量確率1/400を1/200に換算するべき乗則のファクター)で割って18300m3/s程度と推定しています。飽和雨量が48mmでなくもっと大きければ18300m3/s以下になり、八斗島での流下能力16500m3/sと既設6ダムの洪水調節量1000m3/sを考慮すると八つ場ダムの洪水調節量600m3/sは不要になる可能性があると思っています。
利根川の治水安全度1/200における基本高水流量の再計算が楽しみです。関先生のご努力が実って、適切な飽和雨量が決定されることを期待しています。それと共に関東地方整備局には「改訂新版 建設省河川砂防技術基準(案) 同解説 調査編」の確率年の計算式の意味を理解して欲しいと思っています。
努力しても冗長になりました。
うっかりミスでした。