去る11月8日、国交省の政務3役直属の政策審議室(政治主導の実現を目指して民主党政権で新しく設けられた部署とのことです)の方と、基本高水の再検証のプロセスに関して意見交換をする機会がありました。
私は今年の1月から、「利根川の流量計算に使っている飽和雨量の値が48mmというのは全くおかしい。100mm以上で再計算すべきだ」と主張してきました。この問題、自民党の河野太郎議員が国会で質問して下さったことにより、ついに国交省も48mmのパラメータが近年の洪水実績に合致せず、実際には100mm以上であることを認めたのでした。しかるに基本高水は48mmのままで計算していたのです。この事は既に当ブログや他のブログも伝えてきた通りです。
ちなみに2005年当時の審議会で同省は、あたかも昭和33年洪水に当てはまったパラメータが平成10年洪水にも当てはまっているかのように主張していますので、「偽証」の問題が浮上しています。
さて河野議員の国会質問を契機に馬淵大臣が基本高水の再計算を指示したことから、基本高水計算の諸問題に対して私も国交省に意見を述べる機会を与えられたわけです。政策審議室の方は非常に理解力の高い方で、以下に私が述べることのかなりの部分には納得して下さった様子でした(もちろん全部に同意したわけではありませんが・・・・)。
しかし、実際に基本高水の再検証をするのは関東地方整備局です。関東地整の側は、馬淵大臣の意向で動いている政策審議室とは違ったロジックによって動いていると思われます。いかに市民を排除しながら、官僚主導体制を維持して基本高水の再計算を実施するかが最大のポイントになっているのではないかとすら思われるのです。その様子は、以下のブログ記事を読んで知ったことで、私もびっくりしてしまいました。
ダム日記2 扉の先は歴史逆回転で河川官僚天国
http://dam-diary2.cocolog-nifty.com/blog/2010/11/post-620a.html
さて、ジャーナリストのまさのさんが上記ブログで「官僚天国」と形容した八ツ場再検証の場において、関東地整が基本高水の再検証の方向性について提示した案は以下の資料です。紹介いたします。
「八ッ場ダム建設事業の関係地方公共団体からなる検討の場」
「基本高水の検証の進め方(案)」
http://www.ktr.mlit.go.jp/ktr_content/content/000017268.pdf
「新たな流出計算モデルの構築(案)」
http://www.ktr.mlit.go.jp/ktr_content/content/000017271.pdf
以下の文章は、私が国交省に対して提示した案に分かりやすく加筆を施したものです。この私案と、関東地整が提示した案との比較もしながら論じたいと思います。
***********************
1. 情報公開の原則
基本高水流量の再検証はオープンに進めなければならない。計算モデルの全情報を公開し市民の側がチェックできるようにすることが必要。密室で再検証を進めようとする姿勢は、今後ますます国民的合意を得られないだろう。
情報が非公開だと「どうせごまかしてもバレないだろう」という甘えが発生する。国交省が「22000先にありき」で、その数値を維持するため、飽和雨量の値をごまかしてきたのは、情報を隠すことに慣れっこになって甘えが生じていた結果であろう。
今回の「基本高水事件」を契機に、多くの人々が再認識したことは、「情報公開がいかに大事か」ということであった。実際、飽和雨量のパラメータ問題が浮上したのは、八ツ場ダム住民訴訟の原告側が粘り強く情報公開を求めてきた結果であり、それがなければ飽和雨量が48mmで過少であることも国交省以外は誰も知らなかった。さらに、その飽和雨量の値が過少と報道したのは東京新聞であったが、東京新聞が報道しなければ、裁判に関係のない一般の人々は、そうした事実関係がある事も知る由もなかった。
今回の事件は図らずも、情報公開法を改正の動きに弾みをつける結果になったといえる。行政は、国民の税金を使わせていただく以上、その財政支出の根拠になったすべての情報を公開せねばならない。市民の検証にさらすことをおろそかにすれば、いかなる財政支出も納税者の同意を得ることは、今後ますます難しいであろうことを認識せねばならない。
→ 関東地整の案でも「情報公開の徹底」「透明性と客観性の確保」を謳っています。これまで非公開とされてきた「流域分割図」「流出モデル図」も、新たに作成の上公開するとしています。これらの点は評価できます。もっとも、ならば既存の流域分割図が公開できなかったのはなぜなのだという疑念はますます深まりますが・・・
2.カスリーン台風洪水の再来計算に依拠すべきではない
(a)降雨データのいい加減さ
国交省が「利根川の基本高水22000」を決めたもっとも重要な論拠は、カスリーン台風洪水が再来したと仮定して、貯留関数法によって求められる計算流量であると説明されている。しかし、戦後直後の混乱期である1947年(昭和22年)に襲ったカスリーン洪水は、雨量観測値、実測流量観測値とも非常に不確かなデータしかない。この不確かなデータを基に算出されるカスリーンの再来計算に重きを置くべきではない。
1947年当時の雨量観測所の数はわずか13か所しかなく、しかも肝心の洪水ピーク時に機器の故障などでところどころデータが欠損している。データに欠損がなかった観測所はじつに7か所のみである(ちなみに現在は八斗島上流域に150か所以上の雨量観測所がある)。13地点の、しかも欠損だらけの雨量データで八斗島上流域の広大な面積をカバーするのは根本的に無理である。カスリーン洪水の再来計算はもともと精度が低いものであり、不確実である。
実際、カスリーンの再来計算による計算流量が22000に対し、当の1947年の推定実測流量は国交省の数字ですら17000であり、乖離が著しい。計算流量自体が信頼のおける数字ではない。
→ 関東地整は先日示された「新たな流出計算モデルの構築(案)」において、「なお、昭和30年以前に発生した洪水については、現在の雨量観測所と比較して相対的に雨量観測所が少ないことから、洪水毎に等雨量線図を作成する等の制度の向上について検討する」と述べています。
このように、不確かな雨量データをあくまでも使用しようという考えのようです。これに対しては、「いい加減な雨量データの洪水は使うべきではない」と、さらに強く主張したいと思います。
(b)二山型洪水の問題
カスリーン洪水は、一度降雨のピークが来た後に、小降りになり、二度目のピーク降雨が来るという二山型洪水である。二段階モデルの構造からして一山目で飽和雨量に達し、二山目では飽和流出率が1.0として計算される。しかし実際は、一山目と二山目のあいだに降雨が浸透して、土壌の浸透能力が高まっているため、二山目の流出係数は1.0にはならない。おそらく0.7~0.8程度の値と思われる。前回の記事でも解説した「コンクリートタンクの誤謬」である。このため、貯留関数法の二段階モデルでは、二山型洪水の再現計算はうまくできない。カスリーン洪水の計算流量と実測流量の乖離が大きいのも、貯留関数法モデルが二山型洪水の計算に適さないという理由も大きいと思われる。
この事実は河川工学においても定説となっている。権威ある教科書である高橋裕著『新版・河川工学』(東京大学出版会、2008年:73頁)では、「貯留関数法による流出解析は、単一洪水の場合は比較的簡単であるが、ピークが複数の場合には容易ではなく、氾濫する現象にまで適用するのは無理な場がある」と述べられている。教科書でもこのように述べられているのに、それに何ら配慮することなく、国交省は二山型のカスリーン洪水に、安易に貯留関数法を適用し、過大な流量を計算してきたのである。
→ 複数ピーク洪水は貯留関数でうまく計算できないという問題に対して、関東地整は何も述べていません。私は、基本高水を決定する際、複数ピーク洪水は検討対象から外すべきと強く主張したいと思います。
3.総合確率法による基本高水の算出
河川局は「カスリーン洪水の再来計算によって22000立米/秒。総合確率法によって21200立米/秒。安全性を考えて多い方の22000を基本高水とした」と説明してきた。
この総合確率法を使って再計算を実行するのは一つの手段である。これを使う場合、以下の3点を改善することが必要である。
(a)飽和雨量は100mm以上にすること
総合確率法とは、200年に1度確率される319mmの洪水を、さまざまな降雨波形にあてはめた上で、それぞれ貯留関数法によって計算し、それを元に確率論的に洪水流量を求める手法である。
過去の31洪水(昭和49年以前の洪水)を「雨量確率200年に1度」の319mmに引き伸ばし、それぞれ貯留関数法のモデルに当てはめて計算を行い31のピーク流量群を得る。その31のピーク流量群の解析から200年に1度確率の洪水流量として「21200」を得ている。ちなみに319mmに引き伸ばした貯留関数法による31洪水の計算ピーク流量群の単純平均値は17,971であるが、確率論的手法によって、それより3,000以上大きい、21,200が得られている。
このように算出の基礎となる流量は貯留関数法によって求めたものであり、その計算流出モデルはカスリーン台風再来計算と同じく飽和雨量48mmのモデルを使っていると思われる。この飽和雨量の値を現状にあわせて100mm以上にして再計算せねばならない。
→ 飽和雨量100mm以上は、河野議員の国会質問で明らかになった公の事実です。関東地整は、「現在の土地利用状況も反映出来る近年洪水を対象に検討を行い、定数全体を新たに設定する」と述べています。まだ関東地整は、森林保水力の向上により飽和雨量が増加したとは公的に認めていません。このため「森林保水力」や「飽和雨量」という用語の使用は注意深く避けられ、「近年の土地利用」という言葉が使われています。もっとも近年の洪水から定数を設定すれば、飽和雨量は48mmから大幅に引き上がることは確実です。
ちなみに、この総合確率法によれば50年に1度確率の計算流量は16,166と計算されてきました。過去50年間に関しては観測流量が存在しますが、観測流量の最高値は平成10年洪水の9,958立米です(ダムがなかった想定のダム戻し流量)。50年間の実際の最高値が1万以下なのに、総合確率法の50年に1度は1万6000以上なのですから、如何に計算値が過大かがわかるでしょう。この過大さは、飽和雨量が過少という点と、総合確率法の確率論上の問題点の二つの要因によるのではないかと思います。
(b)引き伸ばし率は2倍以下にし、近年の洪水も検討対象に加えること
総合確立法で検討した31洪水のうち19洪水は、引き伸ばし率が2倍を超える。「旧河川砂防技術基準(案)」にあるように以前は2倍以上の引き伸ばしを行わないことがルールとされていた(しかし2005年の改訂版の基準で引き伸ばし2倍以下のルールは削除されている)。
引き伸ばし率を大きくなると、計算流量は過大になりやすい。2倍以下を大きく超える洪水が多数含まれているので、それらを除くことが必要である。2倍以上を除くと、12洪水になる。
また旧建設省が「21200」を求めたのは昭和55年のことであり、それ以降に発生した洪水は検討対象に含まれていない。「引き伸ばし率2倍以下」の基準を守って、昭和55年以降の最近の洪水も含め、さらに飽和雨量は100mm以上に設定して再計算をする必要がある。
→ 2倍以上の引き伸ばしの問題に関しては何も述べられていません。2倍以上の引き伸ばしを禁止することはルールとして確定させる必要があります。この問題は、さらに声を大にして訴えていかねばなりません
(c)「総合確率」という概念の確率論的再検討の必要
総合確率法は関東でのみ使われている手法で、確率論的観点からどこまで科学性があるのかよくわからない。中立な立場の確率論の専門家の意見を聞いて、確率計算の部分も再検討すべきと思われる。
→ 確率論の再検討は何も言及されていません。
4.貯留関数法の再検討 ~二段階モデルから三段階モデルへ
3日雨量300mmを超えるような雨量が頻繁に来週する九州地域の貯留関数法のモデルは、本州のそれとは違う。本州では、一次流出率が0.5で、飽和雨量を超えると飽和流出率が1.0になるといった「2段階モデル」を使用している。
しかし雨量が大きい九州地域では、一次流出率0.4、一次飽和雨量が150で、それを超えると二次流出率が0.8、二次飽和雨量が300といった「三段階モデル」を使用している。雨量の大きい九州では、こうしたモデルにしないと計算値が実測値に当てはまらないからである。
貯留関数法の二段階モデルは200mm程度の中規模洪水には適用できても、大規模降雨に当てはめると計算流量は過大になる傾向がある。実際、300mm程度の豪雨でも、飽和流出率が1.0になるとは考えられない。飽和雨量に達すればあとは雨量の全量が河川に流出するという貯留関数法のモデルは非現実的である。実際には流出係数は大きくなるものの、300mm程度の降雨では100%が流出する流出係数1.0にはなっていないはずである。それを1.0で近似していることが、引き伸ばした際に計算流量が過大になる要因の一つなのだ。それ故、300mm以上の大規模洪水に対しては、本州であっても、雨量の大きい九州で適用しているような三段階モデルを適用した方がよい。
実際の流出曲線は、流出係数は0.2→0.4→0.6・・・・と段階的に増えていき、1.0の漸近線に向かって収束していく。こうした特性を反映した多段階モデルにすれば計算精度は高まるであろう。
→ 二段階モデルから多段階モデルへという論点も、関東地整の資料では何も言及されていませんでした。
5.他の流出解析モデルの適用
貯留関数法は我が国でしか用いられない特殊な流出解析モデルであり、計算精度もそれほど高くないように思われる。
国際的な評価も高いタンクモデル、また最新の分布型モデルなど別のモデルでも計算してみて、貯留関数法で得られた数値と照らし合わせてみる必要がある。
→ 実際には貯留関数法以外のモデルでも検討すれば、貯留関数法の問題点も明らかになり良いとも思われます。しかし関東地整は先手を打って「流出計算モデルは貯留関数法を採用する」と宣言しており、他のモデル使用の可能性にすら言及していません。これは大きな問題です。他のモデルで得られた数値とも突き合わせて検討すべきでしょう。
私は今年の1月から、「利根川の流量計算に使っている飽和雨量の値が48mmというのは全くおかしい。100mm以上で再計算すべきだ」と主張してきました。この問題、自民党の河野太郎議員が国会で質問して下さったことにより、ついに国交省も48mmのパラメータが近年の洪水実績に合致せず、実際には100mm以上であることを認めたのでした。しかるに基本高水は48mmのままで計算していたのです。この事は既に当ブログや他のブログも伝えてきた通りです。
ちなみに2005年当時の審議会で同省は、あたかも昭和33年洪水に当てはまったパラメータが平成10年洪水にも当てはまっているかのように主張していますので、「偽証」の問題が浮上しています。
さて河野議員の国会質問を契機に馬淵大臣が基本高水の再計算を指示したことから、基本高水計算の諸問題に対して私も国交省に意見を述べる機会を与えられたわけです。政策審議室の方は非常に理解力の高い方で、以下に私が述べることのかなりの部分には納得して下さった様子でした(もちろん全部に同意したわけではありませんが・・・・)。
しかし、実際に基本高水の再検証をするのは関東地方整備局です。関東地整の側は、馬淵大臣の意向で動いている政策審議室とは違ったロジックによって動いていると思われます。いかに市民を排除しながら、官僚主導体制を維持して基本高水の再計算を実施するかが最大のポイントになっているのではないかとすら思われるのです。その様子は、以下のブログ記事を読んで知ったことで、私もびっくりしてしまいました。
ダム日記2 扉の先は歴史逆回転で河川官僚天国
http://dam-diary2.cocolog-nifty.com/blog/2010/11/post-620a.html
さて、ジャーナリストのまさのさんが上記ブログで「官僚天国」と形容した八ツ場再検証の場において、関東地整が基本高水の再検証の方向性について提示した案は以下の資料です。紹介いたします。
「八ッ場ダム建設事業の関係地方公共団体からなる検討の場」
「基本高水の検証の進め方(案)」
http://www.ktr.mlit.go.jp/ktr_content/content/000017268.pdf
「新たな流出計算モデルの構築(案)」
http://www.ktr.mlit.go.jp/ktr_content/content/000017271.pdf
以下の文章は、私が国交省に対して提示した案に分かりやすく加筆を施したものです。この私案と、関東地整が提示した案との比較もしながら論じたいと思います。
***********************
1. 情報公開の原則
基本高水流量の再検証はオープンに進めなければならない。計算モデルの全情報を公開し市民の側がチェックできるようにすることが必要。密室で再検証を進めようとする姿勢は、今後ますます国民的合意を得られないだろう。
情報が非公開だと「どうせごまかしてもバレないだろう」という甘えが発生する。国交省が「22000先にありき」で、その数値を維持するため、飽和雨量の値をごまかしてきたのは、情報を隠すことに慣れっこになって甘えが生じていた結果であろう。
今回の「基本高水事件」を契機に、多くの人々が再認識したことは、「情報公開がいかに大事か」ということであった。実際、飽和雨量のパラメータ問題が浮上したのは、八ツ場ダム住民訴訟の原告側が粘り強く情報公開を求めてきた結果であり、それがなければ飽和雨量が48mmで過少であることも国交省以外は誰も知らなかった。さらに、その飽和雨量の値が過少と報道したのは東京新聞であったが、東京新聞が報道しなければ、裁判に関係のない一般の人々は、そうした事実関係がある事も知る由もなかった。
今回の事件は図らずも、情報公開法を改正の動きに弾みをつける結果になったといえる。行政は、国民の税金を使わせていただく以上、その財政支出の根拠になったすべての情報を公開せねばならない。市民の検証にさらすことをおろそかにすれば、いかなる財政支出も納税者の同意を得ることは、今後ますます難しいであろうことを認識せねばならない。
→ 関東地整の案でも「情報公開の徹底」「透明性と客観性の確保」を謳っています。これまで非公開とされてきた「流域分割図」「流出モデル図」も、新たに作成の上公開するとしています。これらの点は評価できます。もっとも、ならば既存の流域分割図が公開できなかったのはなぜなのだという疑念はますます深まりますが・・・
2.カスリーン台風洪水の再来計算に依拠すべきではない
(a)降雨データのいい加減さ
国交省が「利根川の基本高水22000」を決めたもっとも重要な論拠は、カスリーン台風洪水が再来したと仮定して、貯留関数法によって求められる計算流量であると説明されている。しかし、戦後直後の混乱期である1947年(昭和22年)に襲ったカスリーン洪水は、雨量観測値、実測流量観測値とも非常に不確かなデータしかない。この不確かなデータを基に算出されるカスリーンの再来計算に重きを置くべきではない。
1947年当時の雨量観測所の数はわずか13か所しかなく、しかも肝心の洪水ピーク時に機器の故障などでところどころデータが欠損している。データに欠損がなかった観測所はじつに7か所のみである(ちなみに現在は八斗島上流域に150か所以上の雨量観測所がある)。13地点の、しかも欠損だらけの雨量データで八斗島上流域の広大な面積をカバーするのは根本的に無理である。カスリーン洪水の再来計算はもともと精度が低いものであり、不確実である。
実際、カスリーンの再来計算による計算流量が22000に対し、当の1947年の推定実測流量は国交省の数字ですら17000であり、乖離が著しい。計算流量自体が信頼のおける数字ではない。
→ 関東地整は先日示された「新たな流出計算モデルの構築(案)」において、「なお、昭和30年以前に発生した洪水については、現在の雨量観測所と比較して相対的に雨量観測所が少ないことから、洪水毎に等雨量線図を作成する等の制度の向上について検討する」と述べています。
このように、不確かな雨量データをあくまでも使用しようという考えのようです。これに対しては、「いい加減な雨量データの洪水は使うべきではない」と、さらに強く主張したいと思います。
(b)二山型洪水の問題
カスリーン洪水は、一度降雨のピークが来た後に、小降りになり、二度目のピーク降雨が来るという二山型洪水である。二段階モデルの構造からして一山目で飽和雨量に達し、二山目では飽和流出率が1.0として計算される。しかし実際は、一山目と二山目のあいだに降雨が浸透して、土壌の浸透能力が高まっているため、二山目の流出係数は1.0にはならない。おそらく0.7~0.8程度の値と思われる。前回の記事でも解説した「コンクリートタンクの誤謬」である。このため、貯留関数法の二段階モデルでは、二山型洪水の再現計算はうまくできない。カスリーン洪水の計算流量と実測流量の乖離が大きいのも、貯留関数法モデルが二山型洪水の計算に適さないという理由も大きいと思われる。
この事実は河川工学においても定説となっている。権威ある教科書である高橋裕著『新版・河川工学』(東京大学出版会、2008年:73頁)では、「貯留関数法による流出解析は、単一洪水の場合は比較的簡単であるが、ピークが複数の場合には容易ではなく、氾濫する現象にまで適用するのは無理な場がある」と述べられている。教科書でもこのように述べられているのに、それに何ら配慮することなく、国交省は二山型のカスリーン洪水に、安易に貯留関数法を適用し、過大な流量を計算してきたのである。
→ 複数ピーク洪水は貯留関数でうまく計算できないという問題に対して、関東地整は何も述べていません。私は、基本高水を決定する際、複数ピーク洪水は検討対象から外すべきと強く主張したいと思います。
3.総合確率法による基本高水の算出
河川局は「カスリーン洪水の再来計算によって22000立米/秒。総合確率法によって21200立米/秒。安全性を考えて多い方の22000を基本高水とした」と説明してきた。
この総合確率法を使って再計算を実行するのは一つの手段である。これを使う場合、以下の3点を改善することが必要である。
(a)飽和雨量は100mm以上にすること
総合確率法とは、200年に1度確率される319mmの洪水を、さまざまな降雨波形にあてはめた上で、それぞれ貯留関数法によって計算し、それを元に確率論的に洪水流量を求める手法である。
過去の31洪水(昭和49年以前の洪水)を「雨量確率200年に1度」の319mmに引き伸ばし、それぞれ貯留関数法のモデルに当てはめて計算を行い31のピーク流量群を得る。その31のピーク流量群の解析から200年に1度確率の洪水流量として「21200」を得ている。ちなみに319mmに引き伸ばした貯留関数法による31洪水の計算ピーク流量群の単純平均値は17,971であるが、確率論的手法によって、それより3,000以上大きい、21,200が得られている。
このように算出の基礎となる流量は貯留関数法によって求めたものであり、その計算流出モデルはカスリーン台風再来計算と同じく飽和雨量48mmのモデルを使っていると思われる。この飽和雨量の値を現状にあわせて100mm以上にして再計算せねばならない。
→ 飽和雨量100mm以上は、河野議員の国会質問で明らかになった公の事実です。関東地整は、「現在の土地利用状況も反映出来る近年洪水を対象に検討を行い、定数全体を新たに設定する」と述べています。まだ関東地整は、森林保水力の向上により飽和雨量が増加したとは公的に認めていません。このため「森林保水力」や「飽和雨量」という用語の使用は注意深く避けられ、「近年の土地利用」という言葉が使われています。もっとも近年の洪水から定数を設定すれば、飽和雨量は48mmから大幅に引き上がることは確実です。
ちなみに、この総合確率法によれば50年に1度確率の計算流量は16,166と計算されてきました。過去50年間に関しては観測流量が存在しますが、観測流量の最高値は平成10年洪水の9,958立米です(ダムがなかった想定のダム戻し流量)。50年間の実際の最高値が1万以下なのに、総合確率法の50年に1度は1万6000以上なのですから、如何に計算値が過大かがわかるでしょう。この過大さは、飽和雨量が過少という点と、総合確率法の確率論上の問題点の二つの要因によるのではないかと思います。
(b)引き伸ばし率は2倍以下にし、近年の洪水も検討対象に加えること
総合確立法で検討した31洪水のうち19洪水は、引き伸ばし率が2倍を超える。「旧河川砂防技術基準(案)」にあるように以前は2倍以上の引き伸ばしを行わないことがルールとされていた(しかし2005年の改訂版の基準で引き伸ばし2倍以下のルールは削除されている)。
引き伸ばし率を大きくなると、計算流量は過大になりやすい。2倍以下を大きく超える洪水が多数含まれているので、それらを除くことが必要である。2倍以上を除くと、12洪水になる。
また旧建設省が「21200」を求めたのは昭和55年のことであり、それ以降に発生した洪水は検討対象に含まれていない。「引き伸ばし率2倍以下」の基準を守って、昭和55年以降の最近の洪水も含め、さらに飽和雨量は100mm以上に設定して再計算をする必要がある。
→ 2倍以上の引き伸ばしの問題に関しては何も述べられていません。2倍以上の引き伸ばしを禁止することはルールとして確定させる必要があります。この問題は、さらに声を大にして訴えていかねばなりません
(c)「総合確率」という概念の確率論的再検討の必要
総合確率法は関東でのみ使われている手法で、確率論的観点からどこまで科学性があるのかよくわからない。中立な立場の確率論の専門家の意見を聞いて、確率計算の部分も再検討すべきと思われる。
→ 確率論の再検討は何も言及されていません。
4.貯留関数法の再検討 ~二段階モデルから三段階モデルへ
3日雨量300mmを超えるような雨量が頻繁に来週する九州地域の貯留関数法のモデルは、本州のそれとは違う。本州では、一次流出率が0.5で、飽和雨量を超えると飽和流出率が1.0になるといった「2段階モデル」を使用している。
しかし雨量が大きい九州地域では、一次流出率0.4、一次飽和雨量が150で、それを超えると二次流出率が0.8、二次飽和雨量が300といった「三段階モデル」を使用している。雨量の大きい九州では、こうしたモデルにしないと計算値が実測値に当てはまらないからである。
貯留関数法の二段階モデルは200mm程度の中規模洪水には適用できても、大規模降雨に当てはめると計算流量は過大になる傾向がある。実際、300mm程度の豪雨でも、飽和流出率が1.0になるとは考えられない。飽和雨量に達すればあとは雨量の全量が河川に流出するという貯留関数法のモデルは非現実的である。実際には流出係数は大きくなるものの、300mm程度の降雨では100%が流出する流出係数1.0にはなっていないはずである。それを1.0で近似していることが、引き伸ばした際に計算流量が過大になる要因の一つなのだ。それ故、300mm以上の大規模洪水に対しては、本州であっても、雨量の大きい九州で適用しているような三段階モデルを適用した方がよい。
実際の流出曲線は、流出係数は0.2→0.4→0.6・・・・と段階的に増えていき、1.0の漸近線に向かって収束していく。こうした特性を反映した多段階モデルにすれば計算精度は高まるであろう。
→ 二段階モデルから多段階モデルへという論点も、関東地整の資料では何も言及されていませんでした。
5.他の流出解析モデルの適用
貯留関数法は我が国でしか用いられない特殊な流出解析モデルであり、計算精度もそれほど高くないように思われる。
国際的な評価も高いタンクモデル、また最新の分布型モデルなど別のモデルでも計算してみて、貯留関数法で得られた数値と照らし合わせてみる必要がある。
→ 実際には貯留関数法以外のモデルでも検討すれば、貯留関数法の問題点も明らかになり良いとも思われます。しかし関東地整は先手を打って「流出計算モデルは貯留関数法を採用する」と宣言しており、他のモデル使用の可能性にすら言及していません。これは大きな問題です。他のモデルで得られた数値とも突き合わせて検討すべきでしょう。

















第2回の「八ツ場ダム建設事業の関係地方公共団体からなる検討の場」で配布された資料の「基本高水の検証の進め方(案)」と「新たな流出計算モデルの構築(案)」を見る限り、計画論における飽和雨量の見直しがなされることになっていて、これは利根川の基本高水流量問題にとって大きな進歩であると見ています。
この検証がなされると、関東地方整備局がよほどの悪巧みをしない限り、複数のピーク流量群の流量が最近の河川状況に見合った適切なものに改められる結果になると考えます。しかし関先生もご指摘のように、ピーク流量群のどのピーク流量を治水安全度1/200の基本高水流量に決定するかについては、関東地方整備局の業務にはないのでこの問題が残されるようです。
総合確率法で雨量確率1/200に見合うピーク流量群の平均のピーク流量を基本高水流量に決定し、その治水安全度を1/200にしている現行の方法を改めない限り、利根川の治水安全度1/200における適切な基本高水流量は求められないと考えています。
計画雨量まで引き伸ばされた対象降雨から流出計算して求められたピーク流量群のどのピーク流量を治水安全度に見合う基本高水流量に決定するかは、国交省河川局の「河川砂防技術基準」に記述されています。時間的・地域的に発生の可能性がない対象降雨を棄却して、得られたピーク流量群の最大値を基本高水流量に決め、その治水安全度を雨量確率に同じとしています。この考え方はピーク流量群のそれぞれのピーク流量が異なる治水安全度を持つことを全く無視しています。それぞれのピーク流量が異なる治水安全度を持つことは、「基準」の「調査編」に明記されている確率年の計算式からは明白です。しかも最大値を基本高水流量に決定し、その治水安全度を雨量確率と同じであるとすると、基本高水流量が過大になるのは当然です。
総合確率法による基本高水流量の決定法は、関東地方整備局のみで採用されているものですが、利根川のみならず那珂川、久慈川、相模川でも採用されていて、その結果は流量確率で検証されています。総合確率法では雨量確率に見合うピーク流量群の最大値を基本高水流量に決定せず、平均値のピーク流量を基本高水流量に決定しているのは一歩前進していますが、確率年の計算式を適用すると治水安全度は雨量確率の1/2になることを無視しています。
ただ確率年の計算式を適用するに当たっては、計画規模の雨量で実際発生する洪水群を母集団とした場合に、計画雨量まで引き伸ばされた対象降雨からの洪水群を標本と考えたサンプリングの問題を考える必要があります。本来サンプリングは母集団より抜き取った標本について議論すべきですが、引き伸ばされた対象降雨からの洪水群はその意味では純粋なサンプリングの要件を満たしていません。本来のサンプリングでは、標本は母集団を代表していると考えられますが、引き伸ばしサンプリングは母集団を標本が代表しているか疑問が持たれるのは当然です。本来のサンプリングでは母集団の確率分布と標本の確率分布にはバイアス(例えばそれぞれの平均値間の差異)はないと考えますが、引き伸ばしサンプリングではバイアスがあると考えざるを得ないのです。
このバイアスがあることを考慮すると、総合確率法でのピーク流量の平均値(一般的に言ってピーク流量群の平均値)のピーク流量の治水安全度は雨量確率と同じであると考える国交省の立場と、私の主張するピーク流量群の平均値のピーク流量の治水安全度は雨量確率の1/2であるとする立場があることが説明できます。私の立場は確率年の計算式を適用していますが、前提としてバイアスがない、あったとしても無視できるほどに小さいとしていますが、国交省の立場はバイアスがかなりあり、そのバイアス前提で安全率を考慮していると見ることができます。
私はこのバイアスをできるだけ小さくするために、引き伸ばし率2倍程度の制限を外し、できるだけ対象降雨の数を増やすこと、時間的・地域的に発生の可能性がない対象降雨を棄却することをしないサンプリングを提案しています。過去の検討で、利根川の場合には引き伸ばし率3.13倍まで広げ、棄却操作をせずに31モデル洪水を対象にしていたことから、バイアスの悪影響をそれほど気にすることはないと思っています。
なお厄介なことにこのバイアスはまったく偶発的な影響を受けて、同じ引き伸ばされた対象降雨の数でもバイアスが小さいことも大きいこともあることです。最終的には流量確率(再現流量でも可)で治水安全度に見合う基本高水流量の検証を待つことになります。
引き伸ばしを2倍程度に制限する理由として、降雨波形などの特性を損ねるとの見解がありますが、降雨波形の特性は標準化すれば変わることはありません。降雨波形を極めて単純化して正規分布しているとすると、引き伸ばしをしても標準化((雨量-雨量平均値)/標準偏差)すれば、標準化変量は変わりません。またひずみやとがりも変わりません。超過確率の計算はまさに標準化変量でなされますから、特性が変わるとは考えなくてもよいと思います。
また引き伸ばされることでピーク流量が大きくなることは当然ですが、降雨波形が引き伸ばされることで直接ピーク流量が大きくなりことがないことは、上記標準化の過程から明らかでしょう。極めて単純に正規分布を想定しましたが、対数正規分布を考えても同じ結果になります。母数(パラメータ)に線形性が取り入れられる確率分布では標準化の操作は意味があると考えます。
関先生のお説の通りに、総合確率法を含めてピーク流量群からどのピーク流量を治水安全度に見合う基本高水流量に決定するか、そのための前提条件はそのようなものか、河川工学者が知恵を集めて議論すべきです。必要があれば統計学の専門家の意見を聞くことも必要です。この検討については、当然関東地方整備局の活動範囲を越えて国交省河川局の業務の範疇中にあります。国交省河川局に働きかけて、「河川砂防技術基準」に忠実にしたがって確率年の計算式を利用したら、治水安全度に見合う適切な基本高水流量を決定できることを理解してもらうことが必要です。
同時に民主党政権にとってもマニフェストの「コンクリートから人へ」を実行するために政策的に取り上げるべき問題で、利根川の基本高水流量について見直しの英断を下した馬淵大臣の更なる決断も期待するところです
さて、国土交通省八ッ場ダム工事事務所では、一般からの質問や上毛新聞などに掲載された記事についてコメントなどされたものがあります。改めてこれらを読んでおりまして、今では笑えないことが書かれているものがあります。一読されご意見などお聞かせいただければ幸いです。
http://www.ktr.mlit.go.jp/yanba/faq/kenkai2.htm
全文転載
平成16年3月18日付 上毛新聞の「読者のページ」に「八ッ場ダムよりも森林や棚田の整備を」との投稿がありました。
利根川の治水・利水計画は、森林や水田の存在を前提としており、森林や水田の機能とダムの機能があいまって治水・利水面の効用を果たします。このため、ダムの整備と、森林や水田の保全とを両輪として進めていく必要があると考えています。
なお、我が国を代表する科学者からなる日本学術会議の答申によると、「治水上問題となる大雨のときには、洪水のピークを迎える以前に流域は流出に関して飽和状態となり、降った雨のほとんどが河川に流出するような状態になる」ことから、「森林は中小洪水においては洪水緩和機能を発揮するが、大洪水においては顕著な効果は期待できない」とされています。
また、森林は流出を遅れさせ、利用可能な水量を増加させる水資源貯留機能を有しているが、一方で、雨が降らない日が長く続くと、「地域や年降水量にもよるが、河川流況はかえって減少する場合がある」とされています。
このように、森林は、治水・利水計画上、ダムの機能を代替することはできません。水田も、洪水の時にはすでに一杯になって、水を貯めることができなくなってしまうなど、その洪水緩和機能及び水資源貯留機能には限界があるということをご理解願います。
ところで、日本学術会議は、いつ、誰がこのような答申を出したのか全くわかりませんが、ご存知でしょうか。
工事事務所やダム官僚の方の回答パターンは、最初に権威筋の見解と称するものが多いようです。
この解説文を読んで、関先生の見解の正しさと国交省の見解のずさんさを再認識しております。これからも、ブログの更新を楽しみにしております。
追伸
先日は、授業のお手伝いを頂き誠に有難うございました!こちらもダム建設に伴う地すべりリスクの諸問題をわかりやすく解説する資料つくりを行っております。ではでは。
総合確率法の問題に関しては、ご指摘の通り、確率論と統計学の専門家にしっかりと検討してもらえるよう、今後も国交省に働きかけてまいりたいと思います。疑問点は数多くあります。
対象降雨を増やすために引き伸ばしの制限を外すという点に関しては、国交省のこれまでの検証が1974年以前の洪水に限定されていたことから、2倍以下の基準を維持しても1974年以降の洪水を含めればサンプル数は相当に増えると存じます。
日本学術会議の答申に関しては、全くとんでもないいい加減な内容だと思います。作ったのはもちろん、官僚たちが「権威」を持ち出したいときに決まって協力してきた、某T大学の先生です(もちろんT大学が必ず官僚の味方かというとそうでもないことを付言しておきますが・・・・)。
かつては、T大学の先生が主張すると、定説でもないものが、あたかも定説のように一人歩きしてしまったものですが、最近では、「ああ、どうせ御用学者の言うことでしょ。信用に値しませんよ」と軽く流せばよいのではないでしょうか。
緑のダムに関する日本学術会議の言説は、森林は大規模洪水に対しては「顕著な効果は期待できない」、あるいは「降雨量が大きくなると低減する効果は大きくは期待できない」と言います。「顕著」とか「大きくは」とか、何ら数値を示すことなく、万事が抽象的であいまいで、ほとんど何も言っていないに等しい言明です。
「「顕著」とは具体的に何%のことですか?」「大きく期待できない」と言いますが、「20%低減したとしたら、それは大きいのですか、小さいのですか?」と逆に聞けばよろしいのではないかと思います。
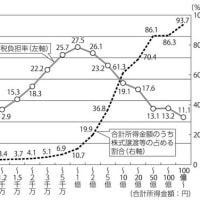
私が東京高裁に出した意見書にもありますが、平成10年洪水の場合、利根川上流のダム6つで7.4%のピークカットです。それに対して、森林は昭和33年から平成10年までの生長分による飽和雨量の増加で20.4%ピークカットしています。
「50%」を「大きい」とか「顕著」とかいうのでしたら、確かに20%はそれに比べて小さいです。しかし、少なくともダム6つの7.4%の効果よりは、はるかに大きいです。
実際には、「大きく期待できない」、「顕著でない」のはダムの治水効果の方です。
下流の伊勢崎市でも、ほとんど観測誤差の範囲内の十数cm程度しかピークは下がらないのですから・・・・。
森林の効果が「顕著でない」と主張する人が、なぜダムの効果を顕著に礼賛できるのか、サッパリわかりません。
http://www.scj.go.jp/ja/info/kohyo/division-5.html の先にPDFファイルがあります。
洪水に関係する話題は、(PDFファイルを表示してもページ番号が見えないのでPDF
の通しページで言うと) 89-93ページにあり、問題の引用は92ページにあります。
ただしこれは「森林の多面的機能」の議論のあとにつけてある「森林の多面的機能各論」の一部です。答申文書の一部にはちがいありませんが、補助的部分のように感じられます。そのような部分から引用して学術会議という権威ある機関のお墨つきがあるように伝えるのはあまり適切ではないと思います。
反面、この文言を、ダムを作りたい役所におもねる御用学者のものだととらえるのも適切でないようにわたしには思われます。否定的表現になってしまっていますが、たとえ健全な森林土壌があっても雨が多くなるほどすぐ流出にまわる割合がふえるという定量的傾向を述べているのだと思います。この表現には森林さえ健全ならば洪水被害の心配はないという過信をいましめようという意図があったかもしれません。