<前回の記事の続きです>
10月12日の馬淵大臣の国会答弁で得られた数値の重要性はもう一点あります。
S33年とS34年では森林保水力はほぼ変わらないにも関わらず、33年が飽和雨量31.77で34年が65と2倍にもなっていることです。これはすごく重要な問題です。
以前の記事(この記事)で、私は、「国交省の誤謬は二つある」と論じました。一つは、これまで論じてきたように森林の生長による保水力の増大を無視していること。二つ目は、過去に観測された中規模洪水に適合したモデルを、観測事例のない仮想の大規模洪水に適用すると計算値は過大になることです。この二つの科学的誤謬を認めず、意図的に使うというトリックを用いて、国交省は基本高水を過大に計算してきました。ここで便宜的に前者を「森林保水力軽視の誤謬」、後者を「引き伸ばしの誤謬」と呼びましょう。前者のトリックの説明は過去記事で十分にしてきたとおりです。
ここで「引き伸ばしの誤謬」の方も解説しておきます。
S33年洪水の際の降雨規模は三日雨量で168㎜で、S34年は216㎜でした。この二つの間には1年の時間しかないので、森林状態はほとんど変化していないはずです。しかしながら、飽和雨量は31.77から65へと2倍以上に増加しています。これは降雨規模の違いが関係しています。降雨規模が大きい集中豪雨型になればなるほど、土壌は、微細な孔隙にまで雨水を最大限に貯めようとします。よってS33年の168㎜の降雨の際に貯留可能だった雨水より、S34年の216㎜の豪雨の際に貯留可能な雨水の量は増大したのです。
このことから判断すると、H10年の186㎜の降雨では飽和雨量が125㎜であっても、カスリーン台風と同規模の318㎜の降雨が襲った場合、土壌が貯留可能な雨水(=飽和雨量)はさらに増えて150㎜くらいになるものと思われます。この論点を、国交省も考慮せねばならないことになります。
「森林保水力軽視の誤謬」と「引き伸ばしの誤謬」の二つを国交省が認めれば、おのずから全国のすべての河川の基本高水は大幅に引き下がることになるのです。

以上の論点を、もう少し詳しく解説します。まず私たちが計算したS33(1958)年洪水とS34(1959)年洪水の実測値と計算値のグラフを掲載しておきます。ともに私が東京高裁に提出した「意見書2」の中にある図14と図15です。
これは国交省が昭和55年に策定した「利根川水系工事実施基本計画」における「流出計算モデル」を、情報公開で得パラメータ・セットを用いて可能な限り忠実に再現したものです。すでに述べてきたように、この「流出計算モデル」の飽和雨量は48㎜でした。
ご覧の通り、S33年洪水のピーク流量は誤差1%でだいたい当てはまるのですが、S34年洪水は誤差が10%出ます。それほどよくは当てはまりません。前の記事で述べたように、国交省はS34年洪水に関しては飽和雨量が65㎜であることを認めました。65㎜にするとピーク流量は適合するのです。
ここで、S33年とS34年は1年しか時間間隔がありません。森林の状態は両年でほとんど変わらないはずなのです。なのになぜ、飽和雨量は違うのでしょうか。
一つの要因が降雨規模の違いなのです。S33年洪水は3日雨量168㎜で、S34年洪水は3日雨量216㎜です。168㎜の洪水を基準に決められた飽和雨量48㎜は、その1.3倍ほどの216㎜の降雨であるS34年洪水には当てはまらないのです。
これが国交省の基本高水が過大である理由の一端です。国交省は168㎜のS33年洪水から得られた飽和雨量48㎜モデルを、総雨量が1.9倍である318㎜のカスリーン洪水に当てはめて「22000」を得ています。
ところが上のグラフにあるようにS33年基準の48㎜モデルの場合、降雨量が1.3倍のS34年洪水に適用すると、計算流量は1.1倍過大な値になっています。カスリーン洪水の場合は、降雨量が1.9倍ですから、上の比率を引き伸ばせば計算流量は1.3倍くらいに過大に算出されていてもおかしくないことになります。実際は非線形現象ですから、その比率を引き伸ばしてはいけないのですが、一次近似としては意味があるでしょう。1.3倍過大に算出されているかも知れない22000を1.3で割るとちょうど17000になります。この17000という値は、まさにカスリーン洪水の際に実際に観測された観測流量(16000から17000のあいだと見られている)にきわめて近い値になるのです。
「引き伸ばしの誤謬」を考慮すれば、昭和33年の森林状態でも基本高水が1.3倍ほど過大に計算されている理由が説明できます。さらに「森林保水力軽視の誤謬」を加味すれば、現在の森林状態における基本高水は17000よりもさらに15~25%低くなるということになります。つまり、現在の森林状態であれば、カスリーン台風と全く同じ豪雨が来ても、15000以上流れることはあり得ないのです。
以下の図は、なぜ、中規模洪水のモデルが大規模洪水に当てはまらないのか、なぜ計算値は過大になるのかの理由の一端を説明するものです。

この図は「流域の保留量曲線」と呼ばれるものです。これは長野県松本市の薄川の観測データから実際に得られた実測値のグラフに、図に示されたような指数関数曲線を最小二乗法であてはめたものです。これは長野県が実施した「森林と水プロジェクト」の調査研究によって作図されたものです。下記サイトの「森林と水プロジェクト」の第二次報告書の第2章にある図を引用させていただきました。
http://www.pref.nagano.jp/rinmu/shinrin/06chisan/02_mori_mizu/index.htm
横軸は一回の降雨イベントごとの総降雨量を示しています。縦軸の「損失量」とは、降った雨のうち、すぐに河川に流出しないで流域(主に森林)に貯留された雨水の量を示します。つまりは、森林土壌などが貯留した雨水の総量のことなのです。
この「流域保留量(損失量)」の値が、河川工学の貯留関数法における「飽和雨量」の値になるのです。
この薄川の事例では、総降雨量100㎜の雨に対して流域保留量(=飽和雨量)は72㎜になり、200㎜の雨に対して飽和雨量は112㎜、300㎜の豪雨に対して飽和雨量は134㎜にまで増大するのです。その理由は、先にも述べたように、降雨規模と強度が大きくなるほど、土壌は、微細な孔隙にまで雨水を最大限に貯めこもうとし、貯留する雨水が増大していくからです。
この図にある薄川流域の場合、流域保留量の値は、最大可能貯留量(=これが本来の意味の飽和雨量)であるところの160㎜の漸近線に向かって収束していきます。
降雨量が増えれば、貯留可能な雨水の量も増えていくということの意味が分かりましたでしょうか?
利根川のS33年洪水に適合する飽和雨量が31.77㎜であったのに対し、降雨量が1.3倍のS34年洪水に適合する飽和雨量が65㎜であった理由の一つはこういうことなのです。
このことから以下のことも成り立ちます。H10年洪水(3日雨量186㎜)に適合する飽和雨量は10月12日の馬淵大臣の国会答弁によれば125mmでした。しかしながら、同じH10年の森林状態であっても、もし3日雨量318㎜のカスリーン級の豪雨がくれば、飽和雨量の値は125㎜よりもさらに増大するはずなのです。どのくらい増大するのかは、近年の降雨イベントから利根川の保留量曲線をつくり、そこから判断すればよいことになります。
中規模洪水からモデルをつくり、そのモデルで大規模洪水を計算すると、計算値は一般的に過大になると私は主張してきましたが、その理由の一端はこういうところにあります。観測された中規模洪水から100㎜の飽和雨量のモデルをつくっても、観測事例のない大規模洪水では、もっと大きい飽和雨量の値を入れて計算せねばなりません。
他にも、貯留関数法には、鉛直地下方向への降雨の浸透を無視しているなど、いろいろなモデル上の欠陥があり、それが基本高水の過大算出を可能にしているのです。
10月12日の馬淵大臣の国会答弁で得られた数値の重要性はもう一点あります。
S33年とS34年では森林保水力はほぼ変わらないにも関わらず、33年が飽和雨量31.77で34年が65と2倍にもなっていることです。これはすごく重要な問題です。
以前の記事(この記事)で、私は、「国交省の誤謬は二つある」と論じました。一つは、これまで論じてきたように森林の生長による保水力の増大を無視していること。二つ目は、過去に観測された中規模洪水に適合したモデルを、観測事例のない仮想の大規模洪水に適用すると計算値は過大になることです。この二つの科学的誤謬を認めず、意図的に使うというトリックを用いて、国交省は基本高水を過大に計算してきました。ここで便宜的に前者を「森林保水力軽視の誤謬」、後者を「引き伸ばしの誤謬」と呼びましょう。前者のトリックの説明は過去記事で十分にしてきたとおりです。
ここで「引き伸ばしの誤謬」の方も解説しておきます。
S33年洪水の際の降雨規模は三日雨量で168㎜で、S34年は216㎜でした。この二つの間には1年の時間しかないので、森林状態はほとんど変化していないはずです。しかしながら、飽和雨量は31.77から65へと2倍以上に増加しています。これは降雨規模の違いが関係しています。降雨規模が大きい集中豪雨型になればなるほど、土壌は、微細な孔隙にまで雨水を最大限に貯めようとします。よってS33年の168㎜の降雨の際に貯留可能だった雨水より、S34年の216㎜の豪雨の際に貯留可能な雨水の量は増大したのです。
このことから判断すると、H10年の186㎜の降雨では飽和雨量が125㎜であっても、カスリーン台風と同規模の318㎜の降雨が襲った場合、土壌が貯留可能な雨水(=飽和雨量)はさらに増えて150㎜くらいになるものと思われます。この論点を、国交省も考慮せねばならないことになります。
「森林保水力軽視の誤謬」と「引き伸ばしの誤謬」の二つを国交省が認めれば、おのずから全国のすべての河川の基本高水は大幅に引き下がることになるのです。

以上の論点を、もう少し詳しく解説します。まず私たちが計算したS33(1958)年洪水とS34(1959)年洪水の実測値と計算値のグラフを掲載しておきます。ともに私が東京高裁に提出した「意見書2」の中にある図14と図15です。
これは国交省が昭和55年に策定した「利根川水系工事実施基本計画」における「流出計算モデル」を、情報公開で得パラメータ・セットを用いて可能な限り忠実に再現したものです。すでに述べてきたように、この「流出計算モデル」の飽和雨量は48㎜でした。
ご覧の通り、S33年洪水のピーク流量は誤差1%でだいたい当てはまるのですが、S34年洪水は誤差が10%出ます。それほどよくは当てはまりません。前の記事で述べたように、国交省はS34年洪水に関しては飽和雨量が65㎜であることを認めました。65㎜にするとピーク流量は適合するのです。
ここで、S33年とS34年は1年しか時間間隔がありません。森林の状態は両年でほとんど変わらないはずなのです。なのになぜ、飽和雨量は違うのでしょうか。
一つの要因が降雨規模の違いなのです。S33年洪水は3日雨量168㎜で、S34年洪水は3日雨量216㎜です。168㎜の洪水を基準に決められた飽和雨量48㎜は、その1.3倍ほどの216㎜の降雨であるS34年洪水には当てはまらないのです。
これが国交省の基本高水が過大である理由の一端です。国交省は168㎜のS33年洪水から得られた飽和雨量48㎜モデルを、総雨量が1.9倍である318㎜のカスリーン洪水に当てはめて「22000」を得ています。
ところが上のグラフにあるようにS33年基準の48㎜モデルの場合、降雨量が1.3倍のS34年洪水に適用すると、計算流量は1.1倍過大な値になっています。カスリーン洪水の場合は、降雨量が1.9倍ですから、上の比率を引き伸ばせば計算流量は1.3倍くらいに過大に算出されていてもおかしくないことになります。実際は非線形現象ですから、その比率を引き伸ばしてはいけないのですが、一次近似としては意味があるでしょう。1.3倍過大に算出されているかも知れない22000を1.3で割るとちょうど17000になります。この17000という値は、まさにカスリーン洪水の際に実際に観測された観測流量(16000から17000のあいだと見られている)にきわめて近い値になるのです。
「引き伸ばしの誤謬」を考慮すれば、昭和33年の森林状態でも基本高水が1.3倍ほど過大に計算されている理由が説明できます。さらに「森林保水力軽視の誤謬」を加味すれば、現在の森林状態における基本高水は17000よりもさらに15~25%低くなるということになります。つまり、現在の森林状態であれば、カスリーン台風と全く同じ豪雨が来ても、15000以上流れることはあり得ないのです。
以下の図は、なぜ、中規模洪水のモデルが大規模洪水に当てはまらないのか、なぜ計算値は過大になるのかの理由の一端を説明するものです。

この図は「流域の保留量曲線」と呼ばれるものです。これは長野県松本市の薄川の観測データから実際に得られた実測値のグラフに、図に示されたような指数関数曲線を最小二乗法であてはめたものです。これは長野県が実施した「森林と水プロジェクト」の調査研究によって作図されたものです。下記サイトの「森林と水プロジェクト」の第二次報告書の第2章にある図を引用させていただきました。
http://www.pref.nagano.jp/rinmu/shinrin/06chisan/02_mori_mizu/index.htm
横軸は一回の降雨イベントごとの総降雨量を示しています。縦軸の「損失量」とは、降った雨のうち、すぐに河川に流出しないで流域(主に森林)に貯留された雨水の量を示します。つまりは、森林土壌などが貯留した雨水の総量のことなのです。
この「流域保留量(損失量)」の値が、河川工学の貯留関数法における「飽和雨量」の値になるのです。
この薄川の事例では、総降雨量100㎜の雨に対して流域保留量(=飽和雨量)は72㎜になり、200㎜の雨に対して飽和雨量は112㎜、300㎜の豪雨に対して飽和雨量は134㎜にまで増大するのです。その理由は、先にも述べたように、降雨規模と強度が大きくなるほど、土壌は、微細な孔隙にまで雨水を最大限に貯めこもうとし、貯留する雨水が増大していくからです。
この図にある薄川流域の場合、流域保留量の値は、最大可能貯留量(=これが本来の意味の飽和雨量)であるところの160㎜の漸近線に向かって収束していきます。
降雨量が増えれば、貯留可能な雨水の量も増えていくということの意味が分かりましたでしょうか?
利根川のS33年洪水に適合する飽和雨量が31.77㎜であったのに対し、降雨量が1.3倍のS34年洪水に適合する飽和雨量が65㎜であった理由の一つはこういうことなのです。
このことから以下のことも成り立ちます。H10年洪水(3日雨量186㎜)に適合する飽和雨量は10月12日の馬淵大臣の国会答弁によれば125mmでした。しかしながら、同じH10年の森林状態であっても、もし3日雨量318㎜のカスリーン級の豪雨がくれば、飽和雨量の値は125㎜よりもさらに増大するはずなのです。どのくらい増大するのかは、近年の降雨イベントから利根川の保留量曲線をつくり、そこから判断すればよいことになります。
中規模洪水からモデルをつくり、そのモデルで大規模洪水を計算すると、計算値は一般的に過大になると私は主張してきましたが、その理由の一端はこういうところにあります。観測された中規模洪水から100㎜の飽和雨量のモデルをつくっても、観測事例のない大規模洪水では、もっと大きい飽和雨量の値を入れて計算せねばなりません。
他にも、貯留関数法には、鉛直地下方向への降雨の浸透を無視しているなど、いろいろなモデル上の欠陥があり、それが基本高水の過大算出を可能にしているのです。














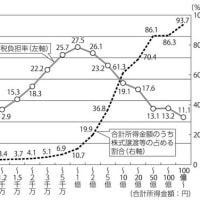



「利根川に関する補足説明資料」資料1 平成17年12月6日 国土交通省 河川局 の7頁にグラフが記載されています。保水機能ありとされている部分が「一次流出率」を表し、勾配が1の直線部分は降雨量がそのまま流出量になる領域です。二つの直線部分の交点の降雨量が飽和雨量です。そして保水機能ありの部分の勾配が「一次流出率」になります。
以上が河川工学における飽和雨量の定義です。森林水文学の表現を使うと流出高=降雨量-損失高になります。損失高と降雨量のグラフを降雨量と流出量のグラフに書き換えると河川工学で言う飽和雨量が求められます。一つの流域においては、シングル イッシューとしての降雨量と流出量のプロットは引用グラフのように散布します。飽和雨量はシングル イッシューの飽和雨量の平均的な値として決定されます。平均的な飽和雨量は一つの流域では一つしか決定されません。したがって降雨量が多くなると飽和雨量も大きくなるとの持論は、河川工学で言う飽和雨量では不適切です。
河川工学での定義にしたがう限り、「引き伸ばしの誤謬」はありません。森林水文学で損失高が飽和雨量であるとの定義にしたがう議論は、河川工学では採用されないでしょう。少なくとも貯留関数法で降雨から流量を計算する場合は、飽和雨量は河川工学の定義にしたがうべきです。
河川工学では、シングル イッシューでの降雨量と計算流量について実測流量と比較して飽和雨量を求めます。このシングル イッシューの降雨量と実績流量の関係からの飽和雨量をそのまま降雨量からの流量の計算に使用することはありません。引用グラフに見られるごとく沢山の降雨量と実測流量の関係から平均的な飽和雨量を求め、その飽和雨量から降雨量と流量の計算を実施します。今回シングル イッシューとして1998年の洪水について飽和雨量が125mmと公表されましたが、この飽和雨量を利用して降雨量から流量を計算するのは早計です。なぜならば125mmの飽和雨量はシングル イッシューの降雨量と実測流量の関係から求められたものであるからです。
降雨量から流量を計算する際の飽和雨量については、多くの降雨量と実測流量から得られた平均的飽和雨量を利用しなければなりません。引用グラフではおおよそ40以上のプロットが見られますが、それだけの降雨量と実測流量の関係から平均的飽和雨量が求められています。
ついでながらカスリーン台風再来時の降雨から基本高水流量22000m3/sを計算した際に飽和雨量を48mmで流出計算してことを「虚構とか捏造」と言われますが、この計算における飽和雨量は1958年の31.77mmと1959年の65mmの平均値48.385mm(丸めて48.39mmもっと丸めて48mm)と考えられるので、そのような表現は不適切であると考えます。対象期間が1937年より1974年といささか古すぎること、僅か二組の降雨量と流量からの平均飽和雨量であることを問題にすべきです。今後利根川の治水安全度1/200における適切な基本高水流量の見直しする際には、できるだけ最新のデータを利用し多くの降雨量と実測流量からの飽和雨量を利用すべきです。
飽和雨量は、本来降雨量、降雨波形、地表の湿潤状態(前期降雨の影響など)により、影響を受けます。勿論森林が荒廃していた時代より手入れが進んだ時代の飽和雨量は大きくなることは予想されます。結論的にはこの二つの考えの両方取り込む必要があります。そして基本高水流量を決定する際の対象期間を先ず決定して、その期間に応じて平均的飽和雨量を決定すべきでしょう。その意味で飽和雨量を100mmであるとするのは、対象期間が不明でありまた平均的飽和雨量である検証もなく、科学的な根拠を欠いていると言えるでしょう。この項は「森林保水力軽視の誤謬」に一部関係しているのは言うまでもありません。
なおカスリーン台風襲来時の計算ピーク流量の治水安全度を1/200であると考えるのは間違いです。確かにカスリーン台風襲来時の降雨量の318mm/3日は計画規模の雨量確率1/200の計画雨量319mm/3日にほぼ同じですから、雨量確率1/200の降雨の際のピーク流量であると言えますが、治水安全度が1/200であるとは言えません。計画雨量まで引き伸ばされた対象降雨からのピーク流量群の棄却後の最大値を基本高水流量に決定し、その治水安全度は雨量確率と同じであるとしてきた国交省の間違った考えをそのまま受け入れています。いずれ利根川の治水安全度1/200における適切な基本高水流量の見直しがされる場合に問題になるでしょう。
以前に飽和雨量を100mmにしてカスリーン台風襲来時のピーク流量を計算したら、 16000m3/s~17800m3/sになったとの鑑定意見書を読んで、この計算の被乗数は22000m3/sでなく、25739m3/sではないかとの質問をメールでした者です。その返事をいただていませんが、コメントへのご返事に合わせていただければ幸いです。
まず、貯留関数法でいう「飽和雨量」はその名にふさわしいものではなく「流域保留量」というべきものであり、それが総降水量が大きくなるほど大きくなるのは当然だ、と言うべきでしょう。そのうえで、流域保留量は総降水量が大きい極限で飽和値(図2-2の例では160mm)をもつと考えられるが、これまでに観測された事例はまだ飽和からは遠いのがふつうだということなのだと思います。なお、図2-2の曲線あてはめは1例の豪雨によるところが大きく定量的に確かとは言えないと思いますが、このような形になるのはもっともだと思います。
「集中豪雨的」と書かれたところはおそらく対象流域の総降水量が大きいことを念頭におかれたのだと思いますが、同じ総降水量でも空間あるいは時間について集中したほうが流域保留量が多くなるという意味に読まれるとまずいです。(後者はどちらかと言えば逆だと思います。 )
流域保留量は鉛直下への降雨の浸透によるものではないでしょうか? そうだとすると貯留関数法も飽和雨量という名前で浸透の効果を扱ってはいることになりますが、その原因に立ち入っていないので根拠をもった数値の決めかたができていない、ということですね。