今、下の図のように、赤い円と青い円があって、その交点
(緑の点)を求めたいとする
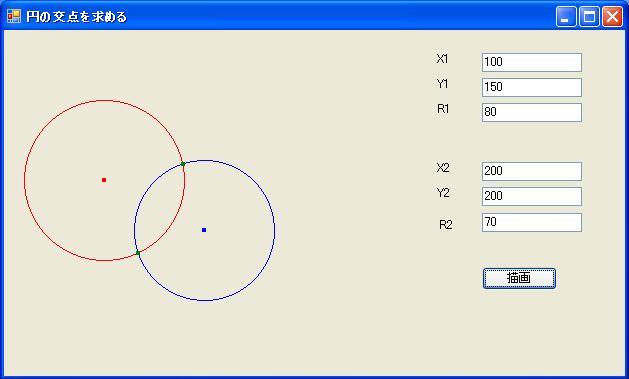
つまり、
赤い円の中心を(x1,y1)半径をr1
青い円の中心を(x2,y2)半径をr2
とする。
このとき、緑色の交点(2つ現れる)(cx1,cy1),(cx2,cy2)を求めよという問題。
この問題をネットで検索する、つまり「円の交点を求める」を調べると
B17.円と円の交点を求める
http://www.hptown.com/ucad/Ufb00017.htm
は美しいものの・・・
ほかは、ぎゃあ・・・式は解きたくない(-_-;)
ってことで、自分で考えてみた。
まず、図のように赤い円の中心をA,青い円の中心をB,円の交点のひとつをCとおく
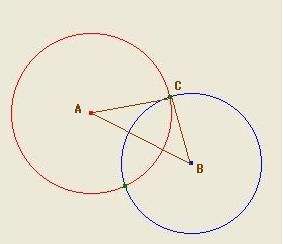
そして、AB,AC,BC間に線を引き
Aが原点になるように平行移動
ABの線をX軸になるように、回転すると、下の図となる。
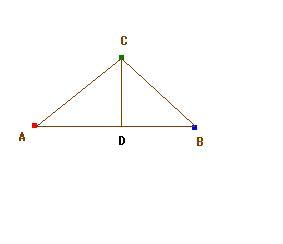
あとあとにために、頂点CからABに対して垂線を引き、その交点をDとします。
■交点までの高さ(Y)を求める
ここで、唐突だけど、この三角形ABCの面積を求めることを考える。
・ひとつはヘロンの公式で求まる
・もうひとつは、1/2*底辺*高さで求まる
ことがわかる
つまり、交点の高さ(=Y座標=高さCDは)
1.ヘロンの公式で、ABCの三角形を求め、
2.三角形の面積=1/2*底辺AB*高さCD
高さCD=2*三角形の面積/底辺AB
で求まる。
ヘロンの公式は、s=1/2(線分AB+線分BC+線分CA)
(線分というのは、線分の長さのこと)としたとき
面積=√(s*(s-線分AB)*(s-線分BC)*(s-線分CA))
で求まる。ここで、
線分ABは、A点とB点の距離
線分BCは、円Bの半径
線分ACは、円Aの半径
なので、sも面積も、求めることができる。これを、2のほうに代入すれば、高さがもとまる
以上により、交点までの高さは求まる
■Xをもとめる
ではつぎに、Xをもとめる。交点からX軸に対して、垂線をおろす。
交点をDとする。Aが原点なので、ADの長さが、Xの値となる。
ここで、 三角形ADCを考える。
線分ACは半径、線分CDは、今求めたYであり、線分CD/線分ACは、sinの関係にある。
このとき、cosは、求めたい線分AD,つまりXの値になる。
そこで、線分CD/線分ADの値をsinとすると、求めたいX(cosは)
X*X+sin*sin=1、X=±√(1-sin*sin)
でもとまる。Xがプラスマイナス2つでる=交点は2つ
これで、X,Yがでた
あとは、元通りに回転移動、原点をAにしたので、元に戻す平行移動をすればいい
うん、ことばでかくと、ぐちゃぐちゃだな。
プログラムだと、かんたんなのに・・・
(緑の点)を求めたいとする

つまり、
赤い円の中心を(x1,y1)半径をr1
青い円の中心を(x2,y2)半径をr2
とする。
このとき、緑色の交点(2つ現れる)(cx1,cy1),(cx2,cy2)を求めよという問題。
この問題をネットで検索する、つまり「円の交点を求める」を調べると
B17.円と円の交点を求める
http://www.hptown.com/ucad/Ufb00017.htm
は美しいものの・・・
ほかは、ぎゃあ・・・式は解きたくない(-_-;)
ってことで、自分で考えてみた。
まず、図のように赤い円の中心をA,青い円の中心をB,円の交点のひとつをCとおく

そして、AB,AC,BC間に線を引き
Aが原点になるように平行移動
ABの線をX軸になるように、回転すると、下の図となる。

あとあとにために、頂点CからABに対して垂線を引き、その交点をDとします。
■交点までの高さ(Y)を求める
ここで、唐突だけど、この三角形ABCの面積を求めることを考える。
・ひとつはヘロンの公式で求まる
・もうひとつは、1/2*底辺*高さで求まる
ことがわかる
つまり、交点の高さ(=Y座標=高さCDは)
1.ヘロンの公式で、ABCの三角形を求め、
2.三角形の面積=1/2*底辺AB*高さCD
高さCD=2*三角形の面積/底辺AB
で求まる。
ヘロンの公式は、s=1/2(線分AB+線分BC+線分CA)
(線分というのは、線分の長さのこと)としたとき
面積=√(s*(s-線分AB)*(s-線分BC)*(s-線分CA))
で求まる。ここで、
線分ABは、A点とB点の距離
線分BCは、円Bの半径
線分ACは、円Aの半径
なので、sも面積も、求めることができる。これを、2のほうに代入すれば、高さがもとまる
以上により、交点までの高さは求まる
■Xをもとめる
ではつぎに、Xをもとめる。交点からX軸に対して、垂線をおろす。
交点をDとする。Aが原点なので、ADの長さが、Xの値となる。
ここで、 三角形ADCを考える。
線分ACは半径、線分CDは、今求めたYであり、線分CD/線分ACは、sinの関係にある。
このとき、cosは、求めたい線分AD,つまりXの値になる。
そこで、線分CD/線分ADの値をsinとすると、求めたいX(cosは)
X*X+sin*sin=1、X=±√(1-sin*sin)
でもとまる。Xがプラスマイナス2つでる=交点は2つ
これで、X,Yがでた
あとは、元通りに回転移動、原点をAにしたので、元に戻す平行移動をすればいい
うん、ことばでかくと、ぐちゃぐちゃだな。
プログラムだと、かんたんなのに・・・
















