今日は線分!
以下のように、青とオレンジの2つの線が交わっている。

このとき、
青の線から距離r1,
オレンジの線から距離r2
離れている線分の交点を求めよ。
■設定
交点を原点になるように平行移動した後、
青い線をX軸になるように回転すると、以下のような感じ。
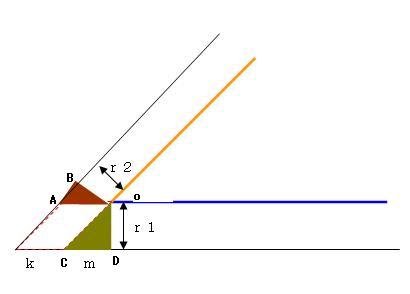
で、青い線からr1(距離分)はなれたところに線を引き、
オレンジのところと、r2離れたところに線を引く
この2つの線分との交点を求めればよい
r1はなれた線上における、
オレンジ線の延長線との交点(c)と、
オレンジからr2はなれた線との交点(頂点)
の距離(=頂点~C)をk、
オレンジの延長線上との交点(c)と、
原点から、r1はなれた線に垂線を下ろした点(D)
までの距離(=CD)をmとおくと、
平行移動&回転された状態で、求める交点は
(-(k+m),-r1)となる。
つまり、k+mを求めればよい
Kについては、茶色い図形で考える。つまり、
O:原点と
A:y=0の線と、オレンジ線からr2はなれた線の交点
B:原点からオレンジ線からr2はなれた線に垂線との交点
の三角形OABを考え、
mについては、緑色の三角形
O:原点と
C:オレンジ線からr1はなれた線の交点
D:原点と青線からr1はなれた線に対して垂線をひいたときの交点
の三角形OCDを考える
■Kについて
オレンジと青の交点のなす各をθとすると、
茶色の図形において
OB/OA=sinθ ここで、OB=r2, OA=kより
r2/k=sinθ k=r2/sinθ
■mについて
OD/OC=sinθ ここで OD=r1, また OCをlとおくと、
r1/l=sinθ なので、 l=r1/sinθ ※
また、m/l=cosθよって、m=lcosθ
これを※の式に入れる
m=(r1*cosθ)/sinθ
■k+mは
k=r2/sinθ
m=(r1*cosθ)/sinθ
k+m=r2/sinθ+(r1*cosθ)/sinθ
=(r2+r1*cosθ)/sinθ
あとは、もとのように回転移動をして、平行移動して、交点の座標を変換する。
うーん、文字で書くと判りにくい。
この式、おもしろくて、90度を超ええると、ぜんぜん違う図になるんだけど、
最終的に出てくる式を変形すると、こうなるんですよ。。。
以下のように、青とオレンジの2つの線が交わっている。

このとき、
青の線から距離r1,
オレンジの線から距離r2
離れている線分の交点を求めよ。
■設定
交点を原点になるように平行移動した後、
青い線をX軸になるように回転すると、以下のような感じ。

で、青い線からr1(距離分)はなれたところに線を引き、
オレンジのところと、r2離れたところに線を引く
この2つの線分との交点を求めればよい
r1はなれた線上における、
オレンジ線の延長線との交点(c)と、
オレンジからr2はなれた線との交点(頂点)
の距離(=頂点~C)をk、
オレンジの延長線上との交点(c)と、
原点から、r1はなれた線に垂線を下ろした点(D)
までの距離(=CD)をmとおくと、
平行移動&回転された状態で、求める交点は
(-(k+m),-r1)となる。
つまり、k+mを求めればよい
Kについては、茶色い図形で考える。つまり、
O:原点と
A:y=0の線と、オレンジ線からr2はなれた線の交点
B:原点からオレンジ線からr2はなれた線に垂線との交点
の三角形OABを考え、
mについては、緑色の三角形
O:原点と
C:オレンジ線からr1はなれた線の交点
D:原点と青線からr1はなれた線に対して垂線をひいたときの交点
の三角形OCDを考える
■Kについて
オレンジと青の交点のなす各をθとすると、
茶色の図形において
OB/OA=sinθ ここで、OB=r2, OA=kより
r2/k=sinθ k=r2/sinθ
■mについて
OD/OC=sinθ ここで OD=r1, また OCをlとおくと、
r1/l=sinθ なので、 l=r1/sinθ ※
また、m/l=cosθよって、m=lcosθ
これを※の式に入れる
m=(r1*cosθ)/sinθ
■k+mは
k=r2/sinθ
m=(r1*cosθ)/sinθ
k+m=r2/sinθ+(r1*cosθ)/sinθ
=(r2+r1*cosθ)/sinθ
あとは、もとのように回転移動をして、平行移動して、交点の座標を変換する。
うーん、文字で書くと判りにくい。
この式、おもしろくて、90度を超ええると、ぜんぜん違う図になるんだけど、
最終的に出てくる式を変形すると、こうなるんですよ。。。
















