放送大学の「微分方程式’23」、わかりました?
私はさっぱり、さっぱりわかりませんでした。
でも、マセマとか見て、
(ただし、自分が見たのは↑のかなり昔の版)
たぶんこんな感じ?というのが掴めたので、
同じ状態の人のために、私の理解を下にかいておきます
(私の理解だから間違ってるかも。
また、今回は途中まで)
■微分方程式の話のおおまかの構造
放送大学の微分方程式なんだけど、これがわからない理由は
・話の中で、何が大事なんだか?
・どこへもっていこうとしているのか
がまったくわからず、話の関連が見えない所。
他の本や授業の講義でも、こうなのかなあ?
これ、まずはじめに、話が、以下の2つに分かれていることに気づかないと、永遠になにを言ってるかわからない。2つとは、以下の2つ
(1)微分方程式は全て解けるというわけではないので、
まず、線形非同次微分方程式という形を、一通りの方式で解く
(放送大学の「微分方程式」のテキストの1章~8章まで、
以下●章と書いたら、この放送大学の「微分方程式」の章のこと)
その時使った技法の発展した話題も、一緒に書いておく
(2)その後、いろいろな別の方法で解いてみる(9章以降)
今回の記事では、(1)だけまとめる。
話しがわかりにくくなっているのは、
・その一通りの方法をはじめに書いてくれてないので、話の流れがわからない
→マセマでは、一階微分方程式の定数変化法という初めの方で
書いてくれているからわかりやすい。放送大学の場合、6章で
ほのめかすけど、最後まではっきり書いていない)
・その割に発展問題の話が延々と続くので、話の本筋が見えず、
余計わけわかんなくなる
のためだと思う。
なので、ここで、まず、
・問題(リサーチクエスチョンRQ)となっている、
線形非同次微分方程式とは何かを説明した後、
・それを解く一通りの方法とは、どういう方法かについて説明してしまおう。
■(8章までの問題)線形非同次微分方程式とは
式自体は、
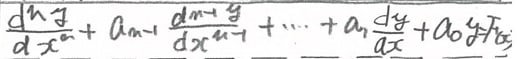
の形、つまり
yをxでn回微分+第n-1の係数 ✖ yをxでn-1回微分 + ・・・
+ 第1の係数 ✖ yをxで1回微分 + 第0の係数✖ y
= Xだけの式(F(x))
( ✖は「かける」の意味で書いてる )
のことを言っている。
また、
yをxで1回微分を1階微分
yをxで2回微分を2階微分
yをxで3回微分を3階微分
:
yをxでn回微分をn階微分といい、
とくに、3階以上の微分をまとめて高階微分という。
■一通りの方法とは
線形非同次微分方程式は一般に、以下の方法でとける
(1)線形非同次微分方程式のxだけの項、つまり、F(x)を0と置いた式、
つまり、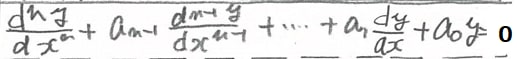
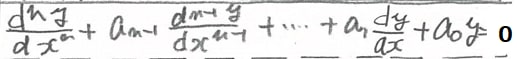
を、随伴方程式というが(マセマでは同次方程式と言っている)、
その随伴方程式を何らかの方法で解く
(2)上記(1)の解は積分しているので、かならずC(任意定数)を
含んでいる。この任意定数Cを、F(x)を使って解く。
このとき解いた解を特殊解という
★(1)の解と、(2)の特殊解を足し合わせたものが、
求める線形非同次微分方程式の解
なお、上記で「解」と言っているのは、任意定数Cを含む解で、このようなCを含む解を一般解といっている。
一般解は随伴方程式の一般解(→上記(1)の解)も、もともとの微分方程式の一般解(→上記(2)の解)の2通りあるが、特に「随伴方程式の一般解」を基本解という。放送大学のテキストでは「随伴方程式の一般解」と書いてあるところも、「基本解」と書いているところとある。
また随伴方程式のように、F(x)の項が0なものを、線形同次微分方程式という。
■話の進め方
話の進め方としては、
・まず一番単純な1階線形非同次微分方程式を解いていく
・次に2階線形非同次微分方程式を解いていく
・高階線形微分方程式については、簡単に解ける定数係数線形微分方程式のみ話題にする
という形になっている。
なお、ここで定数係数線形微分方程式というのを持ち出したが、定数係数とは、線形非同次微分方程式における係数、つまり↓の赤い四角形のところ
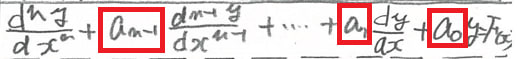
がxをふくまず、すべて定数のものを言います
■で、全体像を示すとこんな感じ

めちゃくちゃ見にくく、わかりにくいので、1階から説明していく
■1階線形非同次微分方程式
こんな形
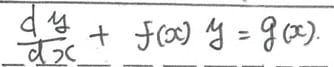
このとき、f(x)yがなければ、y'=g(x)の形で、これは、積分するだけで答えが出る
g(x)が0の時には、線形同次微分方程式の形。この形の場合、
変数分離法っていうのを使うと解ける
では、f(x)もg(x)も0でない場合は、どうするか
それは、上に書いた通り
(1)線形非同次微分方程式のxだけの項、つまり、F(x)を0と置いた式、
を、随伴方程式というが(マセマでは同次方程式と言っている)、
その随伴方程式を何らかの方法で解く
→随伴方程式は、線形同次微分方程式で、それは変数分離法で解ける
(2)上記(1)の解は積分しているので、かならずC(任意定数)を
含んでいる。この任意定数Cを、F(x)を使って解く。
このとき解いた解を特殊解という
→(1)の一般解に含まれるCに対して、C=u(x)と置いて元の式に
代入すると、計算できる。この方法を「定数変化法」という
で、求められるが(というこの方法は放送大学の微分方程式のテキストには書いてないが)、この公式に入れると、一発で答えが出るという公式がある。
あとで掲載する(公式の(1))
■2階線形微分方程式
こんな形
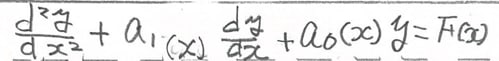
この場合、係数a1,a0がxを含まない定数の場合と、そうでない場合が考えられる。
●定数の場合(定数係数微分方程式)
(1)線形非同次微分方程式のxだけの項、つまり、F(x)を0と置いた式、
を、随伴方程式というが(マセマでは同次方程式と言っている)、
その随伴方程式を何らかの方法で解く
→随伴方程式の微分のところをλとおく
(2階微分のところはλの2乗。λ^2とここでは書く)
つまり、λ^2+a1λ+a0=0を特性方程式と呼ぶが、
この特性方程式を解く。
結果のλによって、一般解が決まる(8.2章定理8.2)
①λが2つの実数解をもつとき
C1 e ^(λ1 x) +C2 e ^ (λ2 x) が一般解 ^ はべき乗のこと。以下同じ
②λが重解を持つとき
C1 e ^(λ x) +C2 x e ^ (λ x) が一般解
③λが虚数解(μ±ν)を持つとき
C1 e ^ (μx) cos ν x + C2 e ^ (μx) sin ν x が一般解
(2)上記(1)の解は積分しているので、かならずC(任意定数)を
含んでいる。この任意定数Cを、F(x)を使って解く。
このとき解いた解を特殊解という
→横書きで書くのは難しいので↓をみてね!

●定数ではないxを含む場合
(1)線形非同次微分方程式のxだけの項、つまり、F(x)を0と置いた式、
を、随伴方程式というが(マセマでは同次方程式と言っている)、
その随伴方程式を何らかの方法で解く
→2階の微分方程式の階数を落として1階の微分方程式にして解く
階数降下法(7.2章)
や
独立変数の変換(7.3章)
によって、計算できるように変換して、一般解を求める
階数降下法は、特殊解がわかっている場合には、公式がある
(2)上記(1)の解は積分しているので、かならずC(任意定数)を
含んでいる。この任意定数Cを、F(x)を使って解く。
このとき解いた解を特殊解という
→定数変化法(Cをu(x)とおき・・・)で求められるが、
(1)で一般解を求めたのであれば、公式を使って、
特殊解を求めることができる
※(1)を階数降下法の公式で、(2)を特殊解を求める公式で解く
・・・ことはできない。(1)の公式を使うには(2)が解けている必要がある。(2)の公式を使うには(1)の解がわかっている必要があるから。
■高階線形微分方程式
●定数係数の場合
2階の場合と同じ。つまり、
(1)線形非同次微分方程式のxだけの項、つまり、F(x)を0と置いた式、
を、随伴方程式というが(マセマでは同次方程式と言っている)、
その随伴方程式を何らかの方法で解く
→随伴方程式の微分のところをλとおいた特性方程式を解く
解いた結果を、2階のところで書いた要領で、一般解にする
(2)上記(1)の解は積分しているので、かならずC(任意定数)を
含んでいる。この任意定数Cを、F(x)を使って解く。
このとき解いた解を特殊解という
→2階のところで書いた通り
●定数係数以外の場合
マセマによると、簡単なケース、特別なケースでないと解けないらしい
実際マセマには、解けるケースが書いてあるのだが、
放送大学の微分方程式のテキストには、書いていない
(高階線形微分方程式のところにはこの解き方ではなく、
基本解と特殊解の関係や、線形性、一般独立の説明としての
ロンスキー行列式について書いている)
■公式
こんな感じ

■その他の話(応用・発展)
●一階線形微分方程式
・変数分離法の応用
同次型(xとyの次数が同じ→u=y/xと置き換えて解く)
f(ax+by+c)の形(ax+bx+cをuと置く。例外あり:2章 2.21式)
・ベルヌーイ方程式
g(x)がg(x) y^nの形→u=y^(1-n)と置く。
→マセマに詳しくやり方書いてある
・リッカチ方程式
・完全微分方程式(4章)
●二階線形微分方程式
解き方というより、微分方程式の性質の話
・リッカチ方程式との関係
・基本解の積の満たす微分方程式
・基本解の商の満たす微分方程式
→シュワルツ微分
気が向いたらというか、自分が理解できて時間があったら、
つづく


















