よく見ると、記事は開立から紹介されていた。

これは開立の時、216の立方根は216の各位の数の和から立方根
すなわち3乗根の3を引くという方法で求まるという。
確かに2+1+6-3=6 で6の3乗は216になる。
343でも3+4+3-2=7となり、7の3乗は343となる。
本当か?
開立の検証は難しそうなので、開平の検証をすることに。

ここでは√25について
25 の各位の数の和 2+5を求めて、2 を引くという。
平方根は2乗根なので2を引くのだ。
で実際に√ の中の数の十の位をa、一の位をbとする
√ の中の数は10a+b
各位の数の和から2を引くと、a+b-2
したがって
√(10a+b) =a+b-2 が成り立つ
これより、
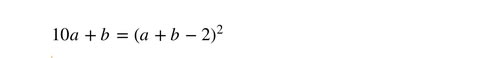
を得るが、これはa, bについての2元2次方程式で、
例のような
(a,b)が(2,5)や(6,4)では成り立つが、(1,6)では成り立たない。
実際、 √16=4 であるが、
1+6-2=5
これはこの「開平法」の反例となる。
したがって、この方法は誤りである。
記事を良く見ると
√25 の次の例は√64となっている。
√36や√49 が飛ばされている!
同様に、この「開立法」も誤りであろう。
で、実際の所、この方法が適用されるのはどんな時か
調べてみた。
つづく

















