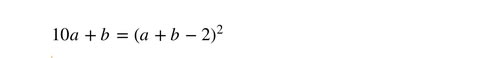おかしな開立法

216の立方根
(2+1+6)-3=6
(各位の数の和)-3 であるという。
例によって百、十、一の位の数をa, b, c とすると
(100a+10b+c)の立方根=(a+b+c)-3
が成り立つと主張している。
ところが、この主張から、
100a+10b+c={(a+b+c)-3}の3乗
が成り立つ。
すなわち

が「いつでも」成り立つという主張だが、
上の式はa,b,cについての3元3次方程式で、
(a, b, c)=(2, 1, 6)がひとつの解であることが分かる。
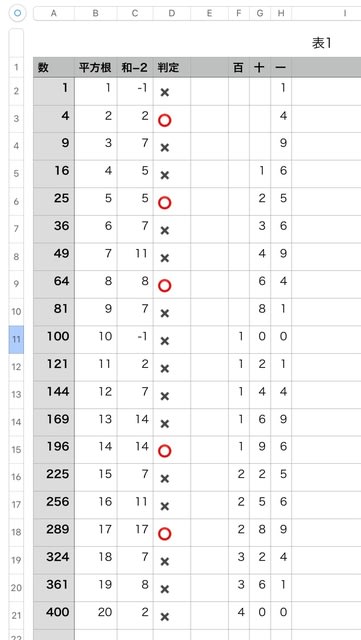
iPadのNumbersで調べてみたところ
100a+10b+cの立方根が整数の場合でも、
上の式が成り立たないという反例が見つかった。

125や343では成り立つが、512、729は成り立たない。
分かりやすい例では1000がある。
したがって、この方法は誤りである。