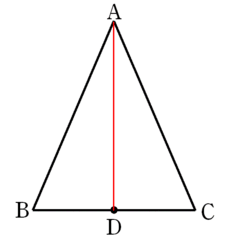
二等辺三角形の底角が等しいことを証明するために引く補助線は、頂角の二等分線だけが正しいと紹介した。図を作る暇がなくて、アップが遅れたことをお許し願いたい。
その理由
中学校の図形といえども一応は「数学」なので,中学生のレベルに合わせて理論
が構築されている。
ユークリッド言論の
共通概念4
重ね合わせることができるものは互いに等しい。
ここから始まる。中学1年では「重ね合わせることができる図形は合同である。」ということを教える。
私は中学2年で図形の証明を習った。そのときは次のような構成になっていた。
「重ね合わせることができる線分や角は等しい。」
ここからスタートして,三角形の合同条件
「2辺とその間の角がそれぞれ等しい三角形は合同」
「1辺とその両端の角がそれぞれ等しい三角形は合同」
この2つは「重ね合わせ」の原理で合同が説明できる。
「3辺がそれぞれ等しい三角形は合同」は重ね合わせでは説明
不可能である。
そこで,
「2辺とその間の角がそれぞれ等しい三角形は合同」
を用いて,二等辺三角形の底角が等しいことを証明し,
「3辺がそれぞれ等しい三角形は合同」を導いていた。
これが,昔の中学校の教科書だった。私もそう習った。
で、その証明とは・・・。これまでに二等辺三角形の底角は等しいことは証明されているとする。

「△ABCと△DEFにおいて
AB=DE,BC=EF,CA=FA であるならば2つの三角形は合同である。」
これを証明する。
(証明)
図のように,△DEFを裏返して,EFがBCに重なるようにする。
AEをひく。
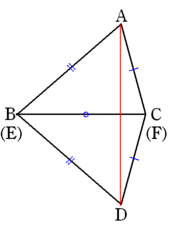
△BDA,△CDAは二等辺三角形であるから,
それぞれの底角 ∠BAD=∠BDA,∠CAD=∠CDA
これら二つの角の左辺同士の和と右辺同士の和は等しいから
∠BAD+∠CAD=∠BDA+∠CDA
したがって,∠BAC=∠BDC=∠EDF
∠BDC=∠EDFであるから∠BAC=∠EDF
以上から,△ABCと△DEFは2辺とその間の角がそれぞれ等しく,合同になる。
(証明終わり)
つまり「3辺相等」を証明するときに「二等辺三角形の底角は等しい」ことを使ったのだ。
ところが,その後の教育課程の改訂により
「三角形の決定条件」なるものが登場し
「三角形の3辺を決定するとその三角形は一意的」を直感で与
えて,上のような構成はしなくなったようだ。
三角形の合同条件のところでは,
「3辺」
「2辺とその間の角」
「1辺とその両端の角」
を一度に教えてしまう。
私はいつもこの提示の仕方には疑問を持っていた。
ユークリッドにしたがえば
「2辺とその間の角」→「二等辺三角形の底角」
→「3辺」という論理構造になっていたのだ。
この立場からすると,ADとして中線ではふさわしくないのだ。
また,Aからの垂線は
「2辺とその間の角」→「二等辺三角形の底角」
→「直角三角形の合同条件」という論理構成が連なっている。
「直角三角形の合同条件」は,
「直角三角形の斜辺と1つの鋭角がそれぞれ等しい」
「直角三角形の斜辺と他の1辺がそれぞれ等しい」
の2つ。
このうち,
「直角三角形の斜辺と他の1辺がそれぞれ等しい」
を使って,△ABDと△ACDの合同が言える。ADが他の1辺。
「直角三角形の斜辺と他の1辺がそれぞれ等しい」の合同条件
は,この条件を満たす2つの三角形を他の1辺を軸として対称
に貼り合わせると,全体が二等辺三角形になることによって証
明される。
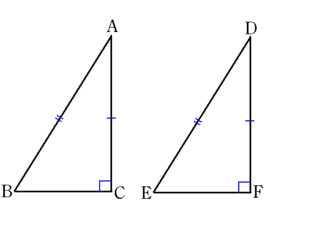
△ABCと△DEFで
∠C=∠F=90度
AB=DE(斜辺)
AC=DF(他の1辺)
この2つの三角形をはりあわせる。

すると△ABEは二等辺三角形になるから、∠B=∠E
ということは残りの角 ∠BAC=∠EAC=∠EDF
一辺とその両端の角がそれぞれ等しい。
二辺とその間の角がそれぞれ等しい。
ということで合同。
というわけで,合同を言う前に「二等辺三角形の底角」を使った
定理を使わなくてはならず,垂線もふさわしくない。
「垂線の場合だと,ピタゴラスの定理を用いて BD = DC が導
かれる」が、「3辺相等」に帰着されていくのでよくない。
なおピタゴラスの定理は三角形の合同条件からは独立している。
ところが,教育現場や教育関係の研究では「中線でも良い」
と主張する人もいる。先ほどの論理に矛盾はあっても生徒の
発見を大事にする立場からなら中線でも許される。
ここらあたりにこだわる教員は少ないと思う。教員3年
目か4年目の頃,卒業生が高校の数学の教科書を持ってきた中
に「二等辺三角形の底角の証明に関して」記載があり、公理など
のことが扱われていて,ほぼ私が主張した事と同じだった。























