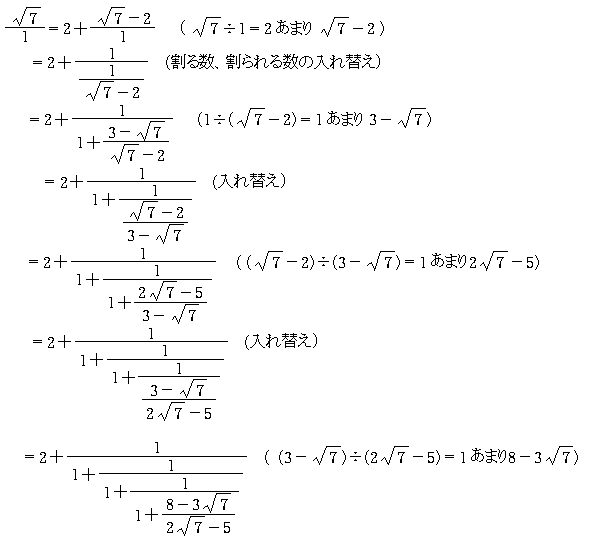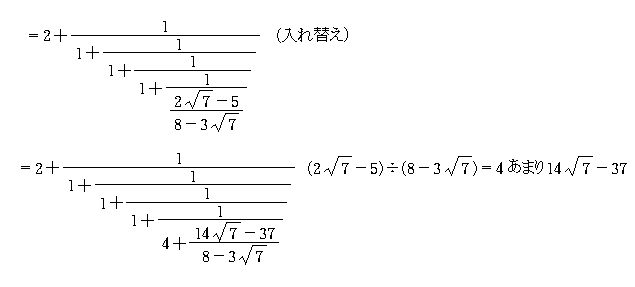質問は
================================================

===================================================
回答・・・問1




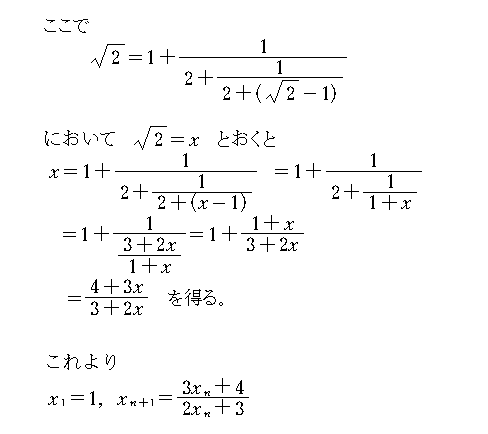
10進Basic というソフトで作ってある。もとはといえばUBASICというソフトに付属のプログラムがあり、これを10進Basicに移植した。私はこのプログラムの原理が分からなくて、ブログにのせて発表したことがあるが、回答は得られなかった。
とにかく便利。お試しあれ。
1.10進Basicのサイトからソフトをダウンロード
2.以下プログラムをコピー&ペーストし、ファイルネームをつけてテキストファイルにしておく。
3.10進Basicでファイルを読み込ませる。(ドラッグ&ドロップでも読める)
4.プログラムを走らせる。
例 ルート7
プログラムを実行すると
n= という入力ウィンドウがでるので、7を入力。
すると、出力テキストウィンドに
n=7
2 [ 1 1 1 4 ]
と出力される。
1 !
2 !
3 ! 2次無理数の連分数展開
4 !
5 !
6 ! filename confra.bas
7 !
8 !
9 !
10 !
20 !
30 !
40 !
50 !
100 !
110 INPUT PROMPT "n=":n
120 IF n=0 THEN STOP
130 LET qn=INT(SQR(n))
140 IF qn=SQR(n) THEN GOTO 500
150 PRINT qn;"[";
160 LET c=n-qn^2
170 LET a=qn
180 LET a1=a
190 LET c1=c
200 ! repeat
210 LET k=INT((qn+a)/c)
220 PRINT k;
230 LET a=c*k-a
240 LET c=INT((n-a^2)/c)
250 IF (a<>a1)OR(c<>c1) THEN GOTO 200
260 PRINT "]"
270 PRINT
280 GOTO 110
290 !
500 PRINT qn;"の2乗です。"
510 PRINT
520 GOTO 110
END


gbさんのコメントに
===============================================================
書籍に記載の 2つの漸化式 の 出生の秘話を (gb) 2010-06-22 11:43:24 連分数絡みで ; http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/000/127698620622516214862.PNG を宜しく お願い致します。 ===============================================================
というのがあった。
さっそくリンクを開いてみた。数学記号を私のほうで編集しなおしてみた。
****リンクの記事***********************************************
*******記事終わり**********************************************
問1はできたので、後日アップする。
問2を見てgbさんの質問のねらいが分かったかも・・・。
問3はもう少し研究が必要。
ところで、gbさんって何者なんだろう?
郵便局の貯金通帳は作ってあったが、カードは作っていなかったので申し込んだ。これで年金を下ろすのも便利になる。ところで年金が振り込まれたことは記事にしたっけ?
6月15日、通帳を持って近所の郵便局へ。ATMで記帳したところ、事前に通知が来ていた通り、年金が振り込まれていた。万歳。
 4月、5月の2ヶ月分の年金である。
4月、5月の2ヶ月分の年金である。60歳で退職後、再任用ということで、正規職員と同じに毎日働いていた。すると、年金の支給は停止されているとの文書が届いていた。働くのを止めてからも、通知で年金停止になっていた。心配してたのだ。
さて、書留でカードが届いたが、配達人は20代の女性。茶髪ではなかったがヤンキーっぽい姉ちゃんだった。郵便局で働く人も幅が広くなったもんだと思った。
早速ATMへ行っておろせるか試す。ATMのメッセージが変わっていた。「通帳またはカードを入れてください」だったか・・・。両方入れたら、カードが戻ってきた。さてはICカードだから読み込みが速いのか、と思った。暗証番号も無事合っていたので、とりあえずおろせた。どうもカードが戻ったのがひっかかった。カードを作ったとき、郵便局の人が「通帳にも暗証番号が記録してあります」と言ったことを思い出した。もしや通帳だけで、カードなしでもおろせるのかと思い、実験。
 「ゆうちょ」は民間の銀行と一味違うのだなと思った。しかし、通帳だけで引き出せるのは危険だと思うのだが、利用者に高齢者が多いためなのだろうか?便利には違いなかったが。
「ゆうちょ」は民間の銀行と一味違うのだなと思った。しかし、通帳だけで引き出せるのは危険だと思うのだが、利用者に高齢者が多いためなのだろうか?便利には違いなかったが。オッテルローへ
クレーラーミュラー美術館でゴッホの絵画を鑑賞。
美術館に向かう道に、クレーラーミュラー氏の像が立っていた。

まずは美術館の庭を散策。あちこちに彫刻がある。
このようなレイアウト方式は、箱根にある「彫刻の森美術館」のモデルとなっているそうだ。
何やら不思議なモニュメントだった。
美術館の中はゴッホの絵が多く展示されていた。大金持ちのクレーラーミュラー氏が買い集めたという。写真はフラッシュを炊かなければOKだ。
ゴッホの跳ね橋、オランダにはこういう跳ね橋があちこちにある。
夜のカフェテラス
というわけで、写真をとりまくったが、ムービーカメラなので、レンズが悪く像がゆがんだ。
フィルムカメラは女房を撮影する専門にしてある。うちの奥さんは風景の中に収まることが好きなので、絵を風景にして何枚も女房を撮影した。ところが、1度操作をミスしてフラッシュが光ってしまった。
大柄な警備員が急いでやってきた。あわてて、Sorry! Mistake! を繰り返した。フィルムを取り上げられるのかと思ったが、許してくれた。フィルムは無事だった。

アムステルダムへ。アムステルダム泊。
ホテルのロビーにあったインターネットにつながるパソコン。結局使わなかった。
部屋にあったLANの設備。パソコンとLANケーブルがあればインターネットにつながるという。
8月20日が終わった。
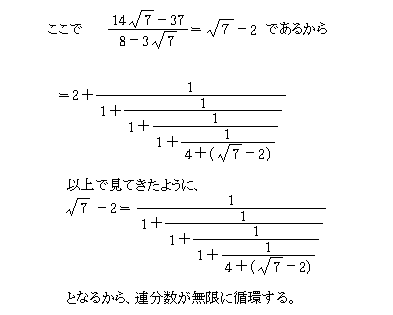
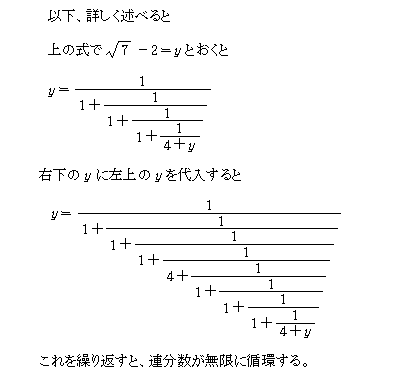
では、√7 の連分数展開をやってみよう。