「ターレスの定理の逆」から「円周角の定理の逆」への発展だが
「定理の逆」について考えなければならない。
ターレスの定理は
半円の円周上のどこに点を取っても、その点と直径の両端を結んで出来る角の大きさは90度である。


一般的な円周角の定理の定理の逆は、4点が同一円周上にあるための条件
「直線ABの同じ側に2点P, Qがあり、∠APB=∠AQBであるとき、4点A,B,P,Qは一つの円周上にある」
という定理だった。
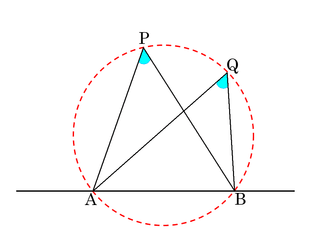
ここでは、ターレスの定理の逆から一般化を試みるので、円周角の定理の逆としては
4点が同一円周上にあるための条件定理ではなく、
およそ教科書にはない定理への一般化を試みる。
そのために「見込む角」という言葉を導入する。
つづく
















