証明「は」と「が」

時間講師をしていたとき、次のような例題の説明をする場面になった。


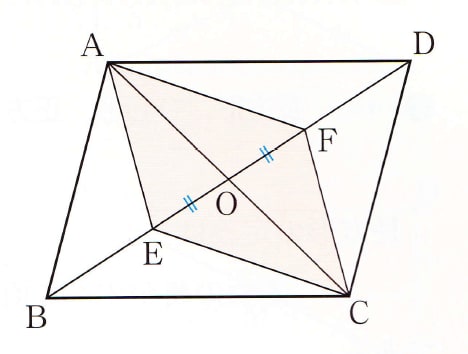
平行四辺形ABCDの対角線の交点をOとし、
対角線BD上に、OE=OFとなるように
２点E、Fをとれば、四角形AECFは平行四辺形に
なります。
このことを証明しなさい。

証明は簡単で
=================================
平行四辺形の対角線は、
それぞれの中点で交わるから
　　　　　OA=OC
仮定から、OE=OF

したがって、対角線がそれぞれの中点で
交わるから、四角形AECFは平行四辺形である。
========================================

教えたのは応用クラスの生徒たちだったので、理解はしてくれたが
「は」と「が」の区別を強調することで、さらに理解が深まったような
気がした。授業にも結構力が入り反応も良かった。


以下、「は」と「が」の区別
========================================
平行四辺形の対角線は、
それぞれの中点で交わるから
　　　　　OA=OC
（平行線の対角線の性質を具体的に表したのが
　OA=OC　なので「は」を使っている。）

仮定から、OE=OF

したがって、対角線がそれぞれの中点で
交わるから、四角形AECFは平行四辺形である。

（OA=OC　と　OE=OF を受けている。対角線が中点で交われば
平行四辺形になるための条件を満たしているので。「が」が使われている。）
=========================================

　こうした言葉の違いを強調すれば、この例題の証明は少しは分かるように
なってくるとは思う。
だが、「平行四辺形の性質」とその逆の「平行四辺形になるための条件」
の違いが分かる応用クラスの生徒たちには良いかもしれないが、
証明そのものが分からない生徒にとってみれば、いくら「は」と「が」
の違いを説明しても納得してはくれないのではないかとも思う。
「仮定」と「結論」の違いが分からないと証明はチンプンカンプンであるからだ。