沖縄続き

二日目
沖縄海洋博跡の公園に行った。ここでは２時間の自由行動だったがかなり広く、一日では周りきれない広さだった。

沖縄

なんと沖縄に来ている。
昨日５日は首里城を見学。
首里城は意外と小ぶりな城だった。


こちらは２０度。暖かい。
これから沖縄海洋博公園に行く。
詳しくは、後日。

角度を求める。補助線

lとmが平行で∠x を求めよ。


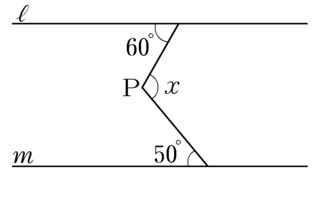
(1)一番紛れのないのは三角形の外角の性質で求める。



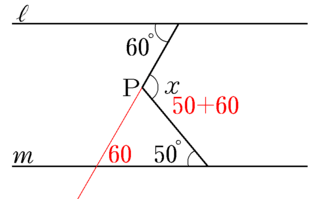
(2) 生徒の何人かは（特に塾などに通っている生徒）


「●が平行線の錯角だから６０度で、×も平行線の錯角だから５０度だから・・・・」

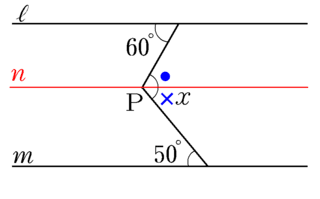
T「ちょっと待って！ nはどっちに平行に引いたの？」とわざと聞く。
生徒「どっちでもいい」「両方に・・・」
T「なんで？」

　ここで生徒たちとの問答を続けました。
　「平行線の平行線は平行線になる」ということばで押さえました。
　この話題は後ほど。


(3) 補助線の引き方で





こういう線を引く生徒が必ず出る。このとき私は「これでは新たな情報が得られないね。角度がわかってこないよ」と言って、「情報が得られる補助線が引けることが大事だ」と押さえていた。
ところがこれでも答えが出せるのでした。それは次の②をやったとき。


②　どんな補助線を引きますか？


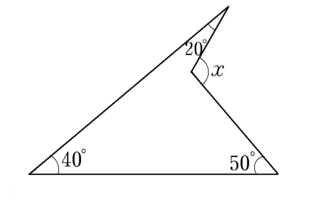
(1)普通はこのように求めるのでしょうか。



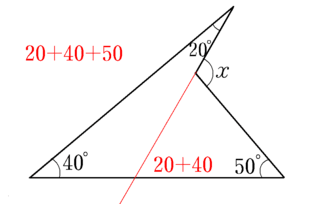
このほか平行線を引くのもありますが、ここでは省略します。


(2)ある生徒が次のような補助線を引いて求めました。



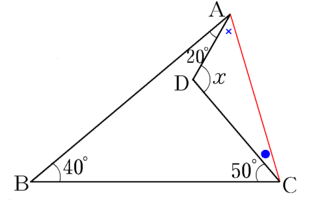
「これでは求められないのでは？」というと
　この生徒は、「求まります。三角形の内角の和が１８０度だから、
＝２０＋４０＋５０＝１１０
全部足せば出ます。」と謎のようなことを言いました。
さて。どう考えたのでしょうか？
そこで私はこうかなと、考えて・・・。
△ABCの内角の和は１８０度であるから，
（２０＋×）＋４０＋（５０＋●）＝１８０
△ADCの内角の和は１８０度であるから，
∠x＋×＋●＝１８０
したがって，
∠x＋×＋●＝２０＋４０＋５０＋×＋●
これより、両辺から×＋●を引けば
∠x＝２０＋４０＋５０＝１１０（度）

　ここの説明は私が、「こういうことかな？」と、こんな風にまとめてしまった。もう少しこの生徒に答えさせればよかったと思いました。


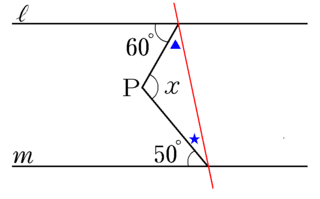
この生徒の発想のおかげで，この問題もこのような補助線を引いても解けることがわかりました。


すなわち，
平行線の性質から
（６０＋▲）＋（★＋５０）＝１８０

三角形の内角の和は１８０度であるから
▲＋∠x ＋★＝１８０

したがって，∠x ＋▲＋★＝６０＋５０＋▲＋★　より

　　　　　　∠x ＝６０＋５０＝１１０（度）

こういう解き方があったなんて・・・。
普通の数学教師なら、とうの昔に気づいているはず。
なのに私はガーン
でした。
生徒に教わった。