相似についてずっと考えていた。中学校の教科書には、
----------------------------------------------------------------
1つの図形を、形を変えずに一定の割合に拡大、または縮小して得られる図形は、
もとの図形と相似であるという。
----------------------------------------------------------------
以前「相似の定義」という記事を書いてそのままになっている。
ここで問題なのは「形を変えずに一定の割合に拡大、または縮小して」ということ。
どうしたらこのような拡大縮小ができるのだろうか。
図の拡大縮小は1点を中心にして次のようにすると良い。すなわち相似変換というものだが、
中学校の教科書ではこの様子を、方眼上の格子点で説明していた。
この図。

ここではOを中心としてOA’=OA×2 という関係で、元の図の1点Aに2倍の拡大図になる点A’を対応させている。
こうして出来た図がこれ。
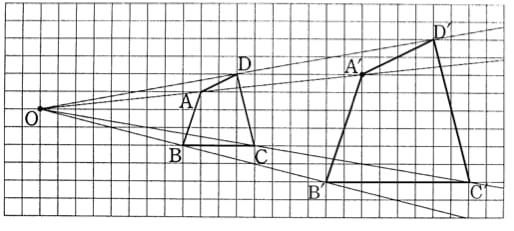
教科書ではこの図を使い拡大図の性質を学ばせている。
ところが、この四角形は格子点を頂点としているので図は一般的ではない。
一般の四角形ではこんな図が考えられる。
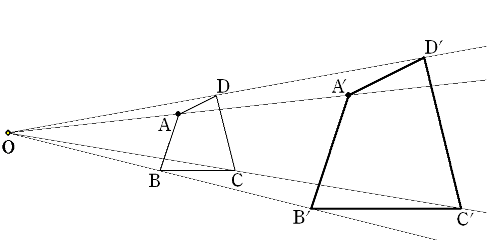
格子点を使っても使わなくても図で、OA’=2OA,OB’=2OB という条件で
A'B'=2AB,A'B'//ABがいえる。
「中点連結定理」を当てはめればよいからだ。
これがいえれば、
同様にして、2つの図の各対応辺の比は一定で1:2となることが保証される。
また各対応辺が平行なことから、平行線の同位角が等しいから、各対応する角はそれぞれ等しいことが保証されることになる。
なぜなら、格子点を使わない図で、B'C'//BC, D'C'//DC
平行線の同位角は等しいから、
角OC'B'=角OCB, 角OC'D'=角OCD
それぞれくわえて、角C'=角C
同様に角A'=角A
対応する辺が平行なことから同位角が等しいので、
それぞれ引けば、角B'=角B。また、角D'=角D
こうして
「対応する角がそれぞれ等しい」ことがいえる。
つまり中点連結定理の結果を認めれば
「対応する辺の比が一定」「対応する角はそれぞれ等しい」が保証される。
こうして、拡大図縮図の性質、相似な図形の性質が導かれる。
しかし、現行の中学数学教科書では「中点連結定理」は、このあと三角形の相似条件を学んでからでてくるので、格子のない図形では説明ができないことになっている。
こういう事情から、格子点を使った説明がされている。
一般の四角形などでは、中点連結定理が使えない。これでは「循環論法」となり不具合を感じないのだろうか?
じつは相似について高校の教科書を調べてみても、きちんとした説明がされてはいない。
















