中学校数学2年の教科書の新旧比較。
旧教科書。
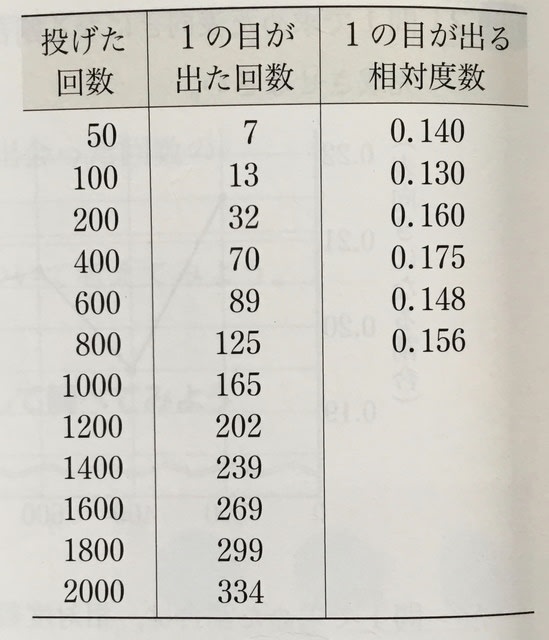
新教科書。

新教科書では相対度数が計算してある。取り扱う場面が多少違うが、資料の数値は変わっていない。(相対度数)=(1の目が出た回数)÷(投げた回数)
たくさんの実験をすると相対度数が落ち着いてくるという主張である。
サイコロを2000回投げるのは大変だから、パソコンで模擬実験をしたことがある。すると、この表のような結果にならなかった。2000回投げて1の目が334回前後になるなどということ、すなわち相対度数がおおむね0.166から0.168くらい(つまり1/6)に収まることは起こらなかった。これは変だと思って確率論の本を引っ張り出して計算してみたところ、2000回程度の実験ではこんな「都合の良い」数値には落ち着いてはくれないことが分かった。
ということで、パソコンで模擬実験。確か30000回投げると投げた実験のうちの90%ほどがこの様な数値になることが分かった(詳しい数値は後日確認してみる)。後に完全退職をして、サイコロを2000回投げたことがある。このことを数学の研究会で発表すると、授業中に実験したことがあるという先生がいた。私立学校の先生であった。私学の教育の自由さを感じた。
実際の理論計算では、教科書にあるような都合の良い結果は10回に1回でもなかなか起こらない。当時は不確かな実験結果を教科書に載せるべきではないと思い憤慨していた。確率はそんなに生やさしいものではないのだ。しかし、歳を取った今では、中学生の発達段階を考慮し、生徒にこのような「夢」を与えて確率の世界に引き込むのだろうと、納得している。数学教育と数学の違いだろう。



























※コメント投稿者のブログIDはブログ作成者のみに通知されます