選択数学から（最大公約数の利用）

　修学旅行の次の日、選択数学の授業で、最大公約数を利用する問題を扱った。

最大公約数を利用する問題
　　例　縦４８cm，横６０cmの長方形があります。この長方形を同じ大きさのできるだけ大きな正方形で敷き詰めたいと思います。１辺が何cmの正方形で敷き詰めれば良いですか。

　　解答　１辺をx cmとすれば，x は４８も６０も割り切ることが出来る数ですから，４８と６０の公約数です。その中でもっとも大きい数ということから，４８と６０の最大公約数であることが分かります。４８と６０の最大公約数を求めて，１２
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１２cm 　

　最大公約数を求めるのに、素因数分解を使うのが普通だが、
例えば１２７１と１５１７の最大公約数を求めることは難しい。
　そこで上のような応用問題を扱って、「互除法」を教えたいと思った。


　できるだけ大きな正方形で敷き詰めることを考えるのに、別の方法を考える。
　まず縦４８cm横６０cmの長方形の中に、出来るだけ大きな正方形を敷く。



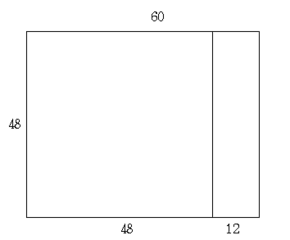
　 当然１辺が４８cmの正方形を敷くことができる。正方形はさらに小さな同じ大きさの正方形で敷き詰めることができるから、残った長方形４８cm×（６０－４８）cmつまり、右側の４８cm×１２cmの長方形が、同一のしかも最大の正方形で敷き詰めることができれば良い。
　
　ところで４８cm×１２cmの長方形は４８÷１２＝４であまりがないから、
１２cm×１２cmの正方形４つでちょうど敷き詰められる。



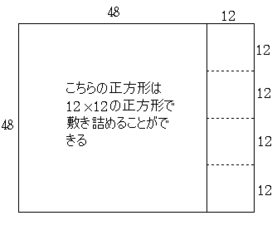
　したがって、４８と６０の最大公約数は１２と分かります。

　 この原理を使って、４１８７と４６６１の最大公約数を求めてみました。
　授業では、黒板に図をかきながら説明しましたが、図が難しいので、ここでは文と式で説明します。

　まず長方形で長い方の辺を縦、短い方を横と決めます。

１．（縦）÷（横）　　４６６１÷４１８７＝１　余り　４７４
　 縦４７４　横４１８７　の長方形が残り、この長方形を１辺が４７４の正方形で敷き詰めます。

２．（横４１８７）÷（縦４７４）＝８　余り　３９５
 縦３９５　横４７４　の長方形が残り、この長方形を１辺が３９５の正方形で敷き詰めます。

３．（横４７４）÷（縦３９５）＝１　余り　７９
　縦７９　横３９５　の長方形が残り、この長方形を１辺が７９の正方形で敷き詰めます。

４．（横３９５）÷（縦７９）＝５　余り　０　でちょうど割り切れます。
  ７９が４１８７と４６６１最大公約数です。
（実際に図をかいて確かめてみて下さい。）
　
　 実際　４１８７＝７９×５３
　　　 　　４６６１＝７９×５９

このように素因数分解出来るのですが、こんな素因数見つかりませんよね。


　 そこで問題（今年度　お茶の水女子大附属高校で出題）

１２７１　１５１７　の最大公約数を求めよ。


この授業を受けた生徒の感想（授業ではここはプリントを使わず余談とした、この次、図を含めたプリントで実際に互除法を教える予定です。）
・最大公約数を求める面白いやり方を知れてよかったです。
・簡単に求められるやり方が分かって良かった。数が大きいと求めるのが大変になると思った。
・最大公約数は素因数分解以外でも求められることが分かった。

簡単に求められるやり方が分かって良かった。と答えた生徒は互除法ではなくて最大公約数を、次のようにして求めるやり方が分かったのかも知れない。
このやり方は、一つ前の授業でやった。 　

　　　　２）　４８　　６０　　 　
　　　　２）　２４　　３０
　　　　３）　１２　　１５
　　　　　　　　４　　　５

　素因数分解が困難な数はこの方法では出来ないので、互除法を使う。
この方法は「ユークリッドの互除法」という。それにしても、面白い方法を古代人は考え出したものである。