============================================================
「長方形を縦横に垂直な線で区切ったときできる4領域について、4領域のうち
2領域の面積の合計がその長方形全体の面積の半分であれば、縦横どちらかの直線
は長方形の中心を通る。」
============================================================
2領域が例えば横に並んでいる場合は明らかなので(縦に並んでいる場合も同様にあきらか)
このように斜めに並んでいる場合を考える。

以下、面積迷路第1集の解答を参考にし、それに付け加えた説明を試みた。
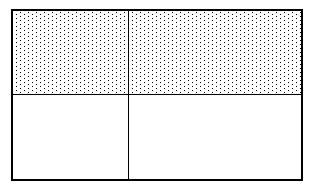
まず縦横の区切りの線が長方形の中心を通っている場合は
(図1)

それぞれの4領域の面積は全体の面積の1/4なので、影をつけた部分の面積の合計は全体の面積の半分になる。
今、区切りの線の交点が左上にずれた場合を考える。

各領域に番号をつけると
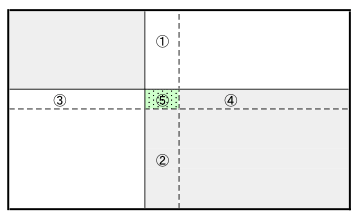
こうなる。
Mac とWin で機種によって文字化けをするので、丸数字の代わりに( )の数字を使う。丸数字1は(1)で表すことにする。
面積迷路第1集の解答では図のように丸数字を使っていた。
上の図で右下の影をつけた部分の面積は図1の時と比べて
(2),(4),(5)の部分の面積だけ大きい。(増えている)
上の図で左上の影をつけた部分の面積は図1の時と比べて
(1),(3),(5)の部分の面積だけ小さい。(減っている)
以上から右下と左上の面積の合計は図1の時と比べて
(2),(4)だけ増えて、(1),(3)減っているから、
{(2)-(1)}+{(4)-(3)}だけ増えていることになる。
縦の長さを比べて (2)の面積>(1)の面積だから、(2)-(1)>0
同様に横の長さから (4)の面積>(3)の面積だから、(4)-(3)>0
したがって、右下と左上の影をつけた部分の面積の合計は
(長方形の半分の面積)+{(2)-(1)}+{(4)-(3)}
以上の準備のもとに性質の確かめに入る。
右下と左上の影をつけた部分の面積の合計は
(長方形の半分の面積)+{(2)-(1)}+{(4)-(3)}
(2)-(1)>0,(4)-(3)>0
この面積の合計が長方形の半分の面積になるためには、
(2)-(1)=0,(4)-(3)=0 が同時に成り立つ必要がある。
縦横の区切りの線の交点は、図のように左上にずれると
長方形の半分の面積を超えてしまう。
(2)-(1)=0,(4)-(3)=0 が同時に成り立つには、区切りの線は
どこに引かなくてはならないかという訳だ。
つづく
















