図で、Lはコイルのインダクタンス、単位はH(ヘンリー)
コイルに流れる電流が1秒間に1アンペアの電流の変化があったときに1ボルトの電圧を生じるとき、
このコイルのインダクタンスは1ヘンリーであるという。
Lヘンリーのコイルはt秒間にIアンペアの電流が変化すれば、
LI/tボルトの電圧が生じる。Δt秒間の瞬間にΔIアンペアの電流変化があれば
LΔI/Δt ボルトの電圧になる。
Rは抵抗単位はオーム、Eは交流電源の電圧で単位はボルトV である。
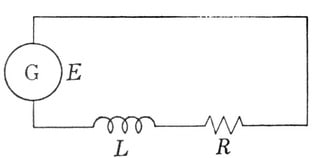
交流電源の電圧を

とすると、キルヒホッフの法則により、

大学時代の物理学の教科書にあった。ここから電流の式を求めるのだが、
教科書では・・・
この方程式を解くために

とおく。微分方程式に代入して、整理すると、次の式が得られる。
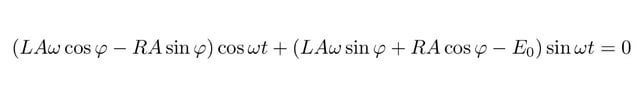
この式が t にかかわらず成り立つには

この2つの式を連立方程式として次の(1)(2)の解を得る。

(1)(2)を2乗して加えると、


また、

これより、

電流は同じ周期を持ち位相がφだけ進んでいることが分かる。
とくにR→0 のとき、すなわちR 抵抗値が0に近づくとき、
tan φ→∞ 無限大に近づくので、φ→π/2
このことは電気回路の本には、「コイルの電流は位相が90度遅れる」などと紹介されている。
また、

であるから、オームの法則 IR=E との比較で

が交流回路における抵抗値を表していると考えられる。

をインピーダンスと言って、交流回路の抵抗値を表す。
私としては、ついにインピーダンスのことが分かったのである。

さて、大学時代の物理学の教科書では、
「電流は電圧と同じ周期を持ちφだけ位相が進んでいる」
などと解説しているが、同じ周期を持つというのは
始めから電流 I を

と置いているのだから当然である。
微分方程式をこのように「視察」つまり「勘」で解の形を
予測し、元の方程式に当てはめて解いたふりをしているのはいただけない。
確かに、導き出した式は元の方程式を満たすので解には違いないのだが、
数学科出身者としては不十分さを禁じ得ない。
次回は微分方程式を実際に解いてみたらどうなったのかを紹介したい。
つづく
















