ターレスの定理の発展３

　

半円のときと同じに二等辺三角形が二つできるが、
∠APBの大きさは青丸と赤丸の合計で、それは

∠Aと∠APBと∠Bの合計の半分である。半円のときは
この合計は180度であったが、今回はそれより」大きいようだ。

で、ここである事実に気付くであろう。



おうぎ形の中心角∠AOBに注目してもらいたい。

∠Aと∠APBと∠Bの合計にさらに中心角∠AOBを加えた合計は
四角形OAPBの内角の和になっている。
四角形の内角の和は360度であるから

∠A＋∠APB＋∠B＋∠AOB＝360度

したがって
∠A＋∠APB＋∠B＝360度-∠AOB

これは図で青く示した角に等しい。


・・・・ということは

∠APBはおうぎ形の中心角の反対側の角の半分であることが分かった。

これにより、点Pをどこに取っても∠APBは中心角の反対側の角の半分となる。

∠APB＝（360度－∠AOB）÷２

したがって一定になる。



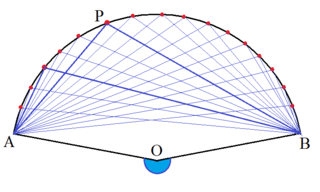
じつはこれは円周角の定理で中心角（青色角）が180度より大きい場合に当てはまっている。



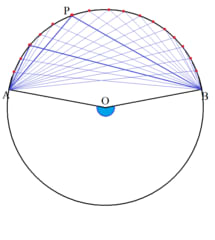
こうしてターレスの定理を一般化することによって円周角の定理が得られたわけである。

では、中心角が180度より小さい場合はどうなのだろうか。

つづく