============================================================
「長方形を縦横に垂直な線で区切ったときできる4領域について、4領域のうち
2領域の面積の合計がその長方形全体の面積の半分であれば、縦横どちらかの直線
は長方形の中心を通る。」
============================================================
縦横の区切りの線が長方形の中心を通っている場合は
(図1)

それぞれの4領域の面積は全体の面積の1/4なので、影をつけた部分の面積の合計は全体の面積の半分になる。
今、区切りの線の交点が左上にずれた場合を考え、各領域に番号をつけると
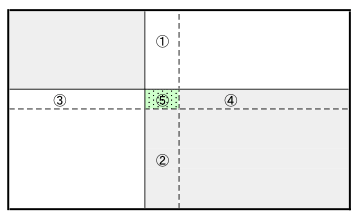
こうなる。
前回確かめたように
右下と左上の影をつけた部分の面積の合計は
(長方形の半分の面積)+{(2)-(1)}+{(4)-(3)}
以上の準備のもとに性質の確かめに入る。
右下と左上の影をつけた部分の面積の合計は
(長方形の半分の面積)+{(2)-(1)}+{(4)-(3)}
(2)-(1)>0,(4)-(3)>0
縦横の区切り線交点がの中心から左上にずれると
斜線部分の面積の合計は(長方形の半分の面積)の半分より大きいことがわかる。
この面積の合計が長方形の半分の面積になるためには、
(2)-(1)=0,(4)-(3)=0 が同時に成り立つ必要がある。
縦横の区切りの線の交点は、図のように左上にずれると
長方形の半分の面積を超えてしまう。
(2)-(1)=0,(4)-(3)=0 が同時に成り立つには、区切りの線は
どこに引かなくてはならないかという訳だ。
そこでまず(2)-(1)=0 であるための条件を調べよう。
そのためには(2)の面積と(1)の面積が等しくなければならないから、
細長い長方形(1)と(2)の縦の長さが等しければよい。
・・・ということは、横の区切り線を(1)(2)の縦の長さが等しくなるように引けばよい。
横の区切り線は長方形の縦の辺の中点を通るように、すなわち長方形の中心を通るように
引けば良いことが分かる。
このとき長方形(3),(4),(5)は消滅して面積が0となるので、
(2)-(1)=0,(4)-(3)=0 が同時に成り立つことが分かる。
同様に、(4)-(3)=0 に注目した場合。縦の線が長方形の中心を通ればよい。
以上から
2領域の面積の合計がその長方形全体の面積の半分であれば、縦横どちらかの直線
は長方形の中心を通ることが分かった。
これで100番の問題を解くための性質は説明出来たが、小学校の算数を使っているが
推論のレベルはかなり高いと思う。
だからこの問題はこうした「禁じ手」使わなければ解けない。
ところで、この性質は中学校入試で使われるのだろうか、疑問が生じた。
============================================================
「長方形を縦横に垂直な線で区切ったときできる4領域について、4領域のうち
2領域の面積の合計がその長方形全体の面積の半分であれば、縦横どちらかの直線
は長方形の中心を通る。」
============================================================
実はこの性質、文字を使って中学校の知識でもっと簡単に証明出来る。それは次回。
つづく



























※コメント投稿者のブログIDはブログ作成者のみに通知されます