今年も4月期の上級ハム国家試験が実施され、この数日で結果発表があったらしい。1アマであれ2アマであれ、合格なさったみなさん、おめでとうございます。特に上級国試に初めて合格なさったみなさんにおかれましては、更に「ようこそ!上級ハムの世界へ!!」と贈らせていただきますね。
それはさておき、Facebookのグループ@八重洲無線のアマチュア無線機が好きな皆様の中で、今回1アマに合格なさった方の報告&コメントに「立体の合成抵抗を求める問題~」と投稿されていて、読んだ瞬間「は?立体?」となり、久々に試験問題をダウンロードしてみた。(ちなみに私は、たぶん直近10年ほどの当該試験問題を一切チェックしていない。)
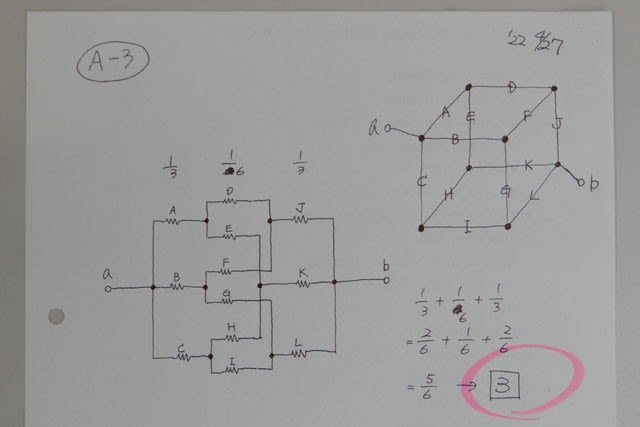
問題用紙をナナメ読みし始めた瞬間、1ページ目のA-3に“らしき図”を見つけた。説明を試みてみると、同じ抵抗を12本使って立方体を作って、一番遠い角と角の間の合成抵抗値を表す式を選ぶという問題だった。確かにコメント投稿者が言うように、私も最初は「???」となった。とりあえず12個の抵抗に記号を振って、普段の2次元的な回路図に落とし込んで考えてみることにする。
見切り発車で記号順に並べて、線で結んでみたらUP写真(←図記号が旧式ですみません…。)のようになったけど、それでも頭がついてこなかったので、とりあえず順追ってみる。①まずaで3又(並列)、②そこから更に2又(並列)が3組、③2又が合流した後に1本と直列になるけど3組のまま、④最後は3組(3又)ともbに合流する、ここまでは分かった。
とりあえず頭の整理は出来たっぽいので、それを数値化(相対値化)してみる。①でaから1/3、②で1/(3×2)、③で1/3、④でbに至る。
次にこれを踏まえて、式を作って計算してみることにした。
合成R=1/3 + 1/(3×2) + 1/3
=2/6 + 1/6 + 2/6
=5/6
解答群を見ると、3番に“5/6・R”があったので、「お~、ちゃんとあるじゃん!」となり、勝手に少し安心感?を得た。ちなみにここまでで10~15分くらいかかったかな?で、早速解答をダウンロード。結果、A-3の正解が“3”とのことで「おっしゃー!」と小声がもれ、更に調子に乗って?蛍光ペンでマルを付けた(笑)。
一方、解答に解説は載っていないので「本当にこういう考え方でイイのかな?」という疑問も少々。まぁ結果的に正解だったので、たぶんOKなんだろう。
-・・・-
と言うことで、久々に上級ハム国試問題で頭の体操をやってみた話でした~。ちなみに、他の問題はチャレンジしていません。あしからず。


























※コメント投稿者のブログIDはブログ作成者のみに通知されます