相似の単元で、「三角形と平行線」のところがある。

図で,DEとBCが平行ならば,AD:AB=AE:AC という有名な定理。
△ADE∽△ABCを使って証明できる。
さて,この逆「AD:AB=AE:AC ならばDEとBCは平行になる。」ということを証明したい。この証明をする問題が教科書にはのっている。
では,この証明をするときに作図はどうするのだろうか。
教科書には「図で,D,EはAD:AB=AE:ACとなるようにとった点です」とある。
ではそのように作図するにはどうするのか?
まずは辺AC上に点Dをとる。それからAD:AB=AE:ACとなるような点Eをとる必要がある。
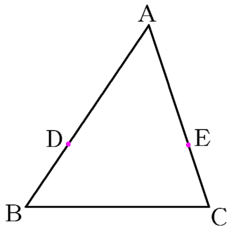
T「点Eの作図はどうするの?」こう発問をしたところ、
生徒は
S「平行線を引けばよい」と答えた。
T「どこを通るどんな平行線?」と聞くと、
S「点Dを通る辺BCに平行な線」という。
T「え?それっていいの?」という。たたみかけるように
T「それを証明しようとしてるんでしょ?」
T「平行線引いちゃったら意味ないじゃないか」
S「・・・」
さて、この作図どうしたらいいでしょうか?
続く

図で,DEとBCが平行ならば,AD:AB=AE:AC という有名な定理。
△ADE∽△ABCを使って証明できる。
さて,この逆「AD:AB=AE:AC ならばDEとBCは平行になる。」ということを証明したい。この証明をする問題が教科書にはのっている。
では,この証明をするときに作図はどうするのだろうか。
教科書には「図で,D,EはAD:AB=AE:ACとなるようにとった点です」とある。
ではそのように作図するにはどうするのか?
まずは辺AC上に点Dをとる。それからAD:AB=AE:ACとなるような点Eをとる必要がある。

T「点Eの作図はどうするの?」こう発問をしたところ、
生徒は
S「平行線を引けばよい」と答えた。
T「どこを通るどんな平行線?」と聞くと、
S「点Dを通る辺BCに平行な線」という。
T「え?それっていいの?」という。たたみかけるように
T「それを証明しようとしてるんでしょ?」
T「平行線引いちゃったら意味ないじゃないか」
S「・・・」
さて、この作図どうしたらいいでしょうか?
続く
















