
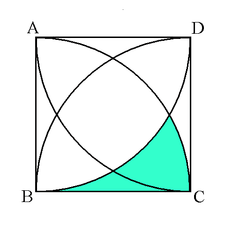
水色の部分の面積4つを正方形の面積から引けば、求める面積が分かる。
図のように補助線BEを引く。
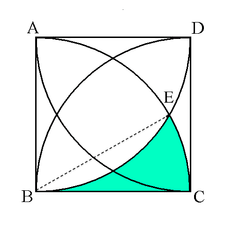
S’=(おうぎ形BEC)ー(月形BE)
=(半径a cmの円の12分の1)ー(月形BE)
=πa^2/12 ー(月形BE)
月形BEは補助線AEを引けば

(月形BE)=(おうぎ形ABE)ー正三角形ABE
=(6分の1の円の面積)ー(正三角形ABE)
=πa^2/6 ー(√3/4)a^2
以上から
S'=πa^2/12 ー(月形BE)
=πa^2/12 ー(πa^2/6 ー(√3/4)a^2)
=(√3/4)a^2ーπa^2/12
したがって、4S'=√3 a^2-πa^2/3
これより S=a^2-(√3 a^2-πa^2/3)
S=(1-√3+π/3) a^2
おわり



























の 4倍 で 1/3 (3-3 Sqrt[3]+π) a^2
「面積と云えば 積分」 と 硬頭學生のなせる 仕業が ↑。
mathnb と 改名致しました。
↑ググり
コメントを お願い致します・
% // FullSimplify // TraditionalForm
=1/3 (3-3 Sqrt[3]+\[Pi]) a^2