空間図形の基本２

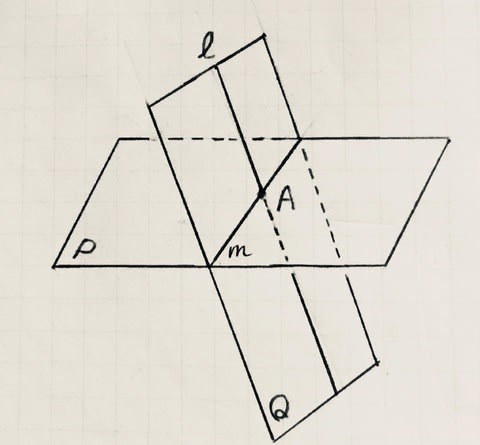
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。


証明

交線m上に２点B、Cを取る。


(1) 点B、Cのどちらか一方が点Aと一致する場合は、点Aは直線m上にある。
　しかも仮定から、点Aはl上にもあるから、l、mの交点である。

(2) 点B、Cのどちらも点Aと一致しない場合、3点A、B、Cについて、
　　3点が一直線上にある場合は、点Aは直線m上にあり、(1)と同様に
　　点Aはl、mの交点である。

(3) ３点が一直線上にない場合、すなわち点Aが直線m上にないとする。
この時は3点A、B、Cによってただ１つの平面が決まる。すなわち
この3点を含む平面はただ１つに限る。

ところが仮定より、点Aは直線lと平面Pの交点だから、平面Pと平面Qにふくまれ、
点B、Cは平面Pと平面Qの交線だから、これらも平面Pと平面Qにふくまれる。

よって、3点A、B、Cは平面Pと平面Qのどちらにもふくまれる。
3点A、B、Cを含む平面はただ１つであるから、
平面Pと平面Qとが一致することになる。
これは平面Pと平面Qとが交わるという仮定に反する。

点Aが直線m上にないと仮定すると、平面Pと平面Qとが交わる
という仮定に反することになるので矛盾が起こった。
よって点Aが直線m上にないということはない。

以上から点Aは直線m上にあり、点Aは直線lとmの交点である。
　　　　　　　　　　　　　　　　　　（証明終）

と、ここまで証明してみたが、よく読み返してみると、
場合分けがくどかった。
(1)と(2)は3点A、B、Cが一直線上にある場合として考えれば、
場合分けは
(1)点Aが直線m上にある場合
(2)点Aが直線m上にない場合
の２つになる。
背理法の証明だから、最初から(2)だけでいいのではないか。
ということで、証明を改良する。

つづく