福島の甲状腺検査で「細胞診76人中10名が陽性、うち3名が摘出して甲状腺がん確定」という問題が話題になっているようです。
NATROMさんの日記
2013-03-15 陽性反応的中割合と「100%引く偽陽性率」を取り違えた甲状腺癌数の推計について
http://d.hatena.ne.jp/NATROM/20130315
2013-03-16 そんで、結局のところ、甲状腺癌の患者数は?
http://d.hatena.ne.jp/NATROM/20130316
この3/15の記事を読んで、これは方程式で解けるはずと思って計算していたら、すでに翌日に解答が記載されていました。
ここでは、
「感度、特異度、検査陽性人数、検査陰性人数が既知の場合の実際の患者数は?」
という一般化した方程式をつくってExcelのシートで色々と代入してみたので、紹介します。
少し前に、
「インフルエンザ検査の陰性的中率」や「新しい母体血出生前検査の陽性的中率」について紹介したので、その続きとも言えます。
まず計算式。いつもの「2×2分割表」。
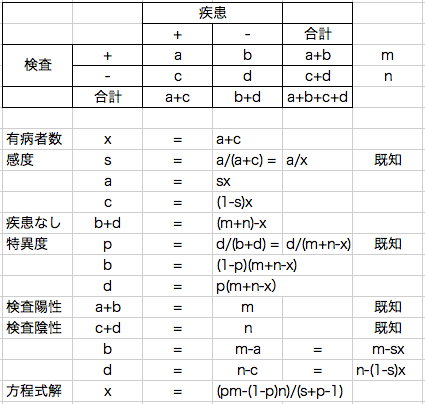
この図の上から順に解いていくとわかるはずなので、詳細は省略します。
本当に病気の人の数(有病者数=a+c)を「x」とします。
感度「s」、特異度「p」の定義から、それぞれaとc、bとdが式で表せます。
検査陽性者数を「m」、陰性者数を「n」とすると、横方向に計算して、bまたはdの式ができます。
bとdについて2つの式ができたので、bまたはdのどちらかで連立方程式を解くと(←どちらでも結果は同じ)、
x=(pm-(1-p)n)/(s+p-1)
となります。
これでabcdが全部決まります。
エクセルのシートに計算式を入れて、数字を動かしてみます。
「感度 s 0.90、特異度 p 0.90、陽性 m 10、陰性 n 66」を入れると、

上記のNATROMさんのページにある計算結果と同じx=3となり、この条件では「検査陽性の10人中3人程度が甲状腺がんである」可能性が高いという結果になります。
有病率(二次精検者の)は3.95%、陽性的中率は27%しかありません。(陰性的中率はほぼ100%)
二次精検(細胞診)までして陽性であっても、更に7割は偽陽性だというのは、確かに受け止め方としては厳しいものがあるかもしれない。
実際にこの数字に近いかどうかはわからないし、ここではそれは問題にしません。
シミュレーションを続けます。
「感度90%、特異度90%」というと、直感的にはこんな数字だと理解しやすいかと思います。
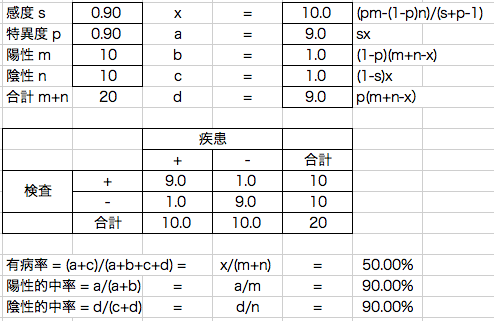
陽性者10人中9人が疾患あり、陰性者10人中9人が疾患なし。
有病率50%、陽性的中率90%。
これは陽的中率が90%で感度・特異度と同じ数字になるのでなんとなく理解しやすいのですが、実際には、陽性的中率は「感度、特異度と有病率」によって大きく変化します。
同じ「感度90%、特異度90%」であっても、有病率が9%まで下がれば陽性的中率は5割を切ってしまう。

元の甲状腺検査に戻ると、二次精検なんだから一般的には「感度99%、特異度99%」くらいのイメージを持ってしまう。

もしそうだとしたら、この表にあるように「10人中9人強が疾患あり、陽性的中率93.4%」となって期待通りの数値が得られるのですが、こうしてみると「感度90%、特異度90%」というのはかなり低い数字だということがわかる。
この「感度90%、特異度90%」は確定した数字ではなく、「偽陽性・偽陰性10%未満」という記載のようです。「感度95%、特異度95%」に上げてみると、a=6.5 c=0.3 x=6.9(四捨五入しているため足し算が合わない)となり、あと4人程度のがん患者含まれていてもおかしくない。
穿刺吸引細胞診で取り逃しはあっても誤ってがんと診断する可能性はゼロに近いという前提で、感度80%(見逃しが20%)、特異度99.9%(偽陽性なし)とすると a=9.9 c=2.5 x=12.4となり、10人よりも多い可能性ありという元の話に近くなる。
いずれも、仮定の話です。
一方、一次スクリーニング検査では、有病率0.01%(10万人あたり10人)程度の疾患を検出しようとすると、「感度100%(取りこぼしゼロ)、特異度99.9%」という優秀な検査であっても、陽性的中率は1割にも満たない。9割は偽陽性ということになる。

この数字をどう評価するかは、検出すべき病気の性質(決して見逃してはいけない、もし見逃したら次の検査までに進行して手遅れになる病気かどうか)によって違ってきます。
(甲状腺エコー検査がこの数字にあてはまるという意味ではなく、あくまで一次スクリーニング検査一般についてのシミュレーションです)
感度、特異度、有病率(見込み)の数字だけでなく、実際には小児の甲状腺がんの性質や進行スピードなどが問題になって来るのですが、勉強不足なのでこの点についてはコメントできません。
このような検査の性質をあらかじめ理解して、偽陽性が検査によって相当の割合で発生するということを前提として話を進めるべき、というのが当面の結論か。
(このExcelのシートは結構便利)
追記:(誤解無きよう念のため)甲状腺がんが3人だけで7人は違うという意味ではなく、4~10人(あるいはそれ以上)のいずれの可能性も否定できません。感度・特異度が安定している検査でも、確率的にバラツキは当然あり得るので。
追記2:OurPlanet-TVで津田先生が言っているように、甲状腺がん3人確定という「多発」状況にあり、今後の変動について厳しい目で見ていく必要があり、7人についても定期的な経過観察が必要なことは当然です。
NATROMさんの日記
2013-03-15 陽性反応的中割合と「100%引く偽陽性率」を取り違えた甲状腺癌数の推計について
http://d.hatena.ne.jp/NATROM/20130315
2013-03-16 そんで、結局のところ、甲状腺癌の患者数は?
http://d.hatena.ne.jp/NATROM/20130316
この3/15の記事を読んで、これは方程式で解けるはずと思って計算していたら、すでに翌日に解答が記載されていました。
ここでは、
「感度、特異度、検査陽性人数、検査陰性人数が既知の場合の実際の患者数は?」
という一般化した方程式をつくってExcelのシートで色々と代入してみたので、紹介します。
少し前に、
「インフルエンザ検査の陰性的中率」や「新しい母体血出生前検査の陽性的中率」について紹介したので、その続きとも言えます。
まず計算式。いつもの「2×2分割表」。

この図の上から順に解いていくとわかるはずなので、詳細は省略します。
本当に病気の人の数(有病者数=a+c)を「x」とします。
感度「s」、特異度「p」の定義から、それぞれaとc、bとdが式で表せます。
検査陽性者数を「m」、陰性者数を「n」とすると、横方向に計算して、bまたはdの式ができます。
bとdについて2つの式ができたので、bまたはdのどちらかで連立方程式を解くと(←どちらでも結果は同じ)、
x=(pm-(1-p)n)/(s+p-1)
となります。
これでabcdが全部決まります。
エクセルのシートに計算式を入れて、数字を動かしてみます。
「感度 s 0.90、特異度 p 0.90、陽性 m 10、陰性 n 66」を入れると、

上記のNATROMさんのページにある計算結果と同じx=3となり、この条件では「検査陽性の10人中3人程度が甲状腺がんである」可能性が高いという結果になります。
有病率(二次精検者の)は3.95%、陽性的中率は27%しかありません。(陰性的中率はほぼ100%)
二次精検(細胞診)までして陽性であっても、更に7割は偽陽性だというのは、確かに受け止め方としては厳しいものがあるかもしれない。
実際にこの数字に近いかどうかはわからないし、ここではそれは問題にしません。
シミュレーションを続けます。
「感度90%、特異度90%」というと、直感的にはこんな数字だと理解しやすいかと思います。

陽性者10人中9人が疾患あり、陰性者10人中9人が疾患なし。
有病率50%、陽性的中率90%。
これは陽的中率が90%で感度・特異度と同じ数字になるのでなんとなく理解しやすいのですが、実際には、陽性的中率は「感度、特異度と有病率」によって大きく変化します。
同じ「感度90%、特異度90%」であっても、有病率が9%まで下がれば陽性的中率は5割を切ってしまう。

元の甲状腺検査に戻ると、二次精検なんだから一般的には「感度99%、特異度99%」くらいのイメージを持ってしまう。

もしそうだとしたら、この表にあるように「10人中9人強が疾患あり、陽性的中率93.4%」となって期待通りの数値が得られるのですが、こうしてみると「感度90%、特異度90%」というのはかなり低い数字だということがわかる。
この「感度90%、特異度90%」は確定した数字ではなく、「偽陽性・偽陰性10%未満」という記載のようです。「感度95%、特異度95%」に上げてみると、a=6.5 c=0.3 x=6.9(四捨五入しているため足し算が合わない)となり、あと4人程度のがん患者含まれていてもおかしくない。
穿刺吸引細胞診で取り逃しはあっても誤ってがんと診断する可能性はゼロに近いという前提で、感度80%(見逃しが20%)、特異度99.9%(偽陽性なし)とすると a=9.9 c=2.5 x=12.4となり、10人よりも多い可能性ありという元の話に近くなる。
いずれも、仮定の話です。
一方、一次スクリーニング検査では、有病率0.01%(10万人あたり10人)程度の疾患を検出しようとすると、「感度100%(取りこぼしゼロ)、特異度99.9%」という優秀な検査であっても、陽性的中率は1割にも満たない。9割は偽陽性ということになる。

この数字をどう評価するかは、検出すべき病気の性質(決して見逃してはいけない、もし見逃したら次の検査までに進行して手遅れになる病気かどうか)によって違ってきます。
(甲状腺エコー検査がこの数字にあてはまるという意味ではなく、あくまで一次スクリーニング検査一般についてのシミュレーションです)
感度、特異度、有病率(見込み)の数字だけでなく、実際には小児の甲状腺がんの性質や進行スピードなどが問題になって来るのですが、勉強不足なのでこの点についてはコメントできません。
このような検査の性質をあらかじめ理解して、偽陽性が検査によって相当の割合で発生するということを前提として話を進めるべき、というのが当面の結論か。
(このExcelのシートは結構便利)
追記:(誤解無きよう念のため)甲状腺がんが3人だけで7人は違うという意味ではなく、4~10人(あるいはそれ以上)のいずれの可能性も否定できません。感度・特異度が安定している検査でも、確率的にバラツキは当然あり得るので。
追記2:OurPlanet-TVで津田先生が言っているように、甲状腺がん3人確定という「多発」状況にあり、今後の変動について厳しい目で見ていく必要があり、7人についても定期的な経過観察が必要なことは当然です。











http://www.env.go.jp/press/press.php?serial=16520
数字見直してからあとで別に書きたいとは思いますが。
兵庫でも?な結果みたいなので・・・
「神戸での小児甲状腺超音波検査の試み」
http://rokko-mcoop.sakura.ne.jp/sblo_files/rokko-news/image/E58AB4E5838DE88085E4BD8FE6B091E58CBBE79982E38080E7A59EE688B8E381A7E381AEE5B08FE58590E794B2E78AB6E885BAE8B685E99FB3E6B3A2E6A49CE69FBBE381AEE8A9A6E381BF.pdf