長野旅行9月17日（金）の２

　栂池自然園ハイキング出発。前回は時間の制約があったので途中で引き返したが、今回は１日自由。帰りのロープウェイの最終４時２０分に乗ればよい。

ミヤマトリカブト　深山鳥兜　　この花は良く見かけた。毒草。


一瞬晴れて、山がよく見えた。反対側の白馬岳方面は残念ながら晴れていない。


水ばしょう湿原。水芭蕉の葉は結構大きい。


セリ科の良く似た植物が多い。ミヤマシシウド　深山猪独活　か・・・。


遠くに自然園の入り口が見える


ナナカマドの紅葉


これまでは木道を歩いてきたが、前回引き返した場所を過ぎ、いよいよ山登りコースへ。
「その靴で大丈夫？」と書いてある。


トイレ。このあとはトイレがない。ここを過ぎたが、帰りにまた通ったので使った。きれいに整備されていた。


山道を登った。沢の所。石がごろごろしていた。登ること40分ぐらいか。
途中の池。ここまで来てから引き返す人もいたが、せっかく来たのでもうひと頑張り。


やっと「展望湿原」というところに到着。
あたりはガスが立ちこめる。晴れていれば目の前に白馬岳の連峰が見えるはず。


ここでお弁当。ホテル謹製。1050円。竹製のかごに入っていておしゃれ。


鶏の唐揚げ、ゆで卵、おにぎり、魚のフライなど


　ここには大勢の客が写真を撮ったり、弁当を食べていたりしていた。金曜日の平日とあって、ほとんどが中高年。しかも定年退職後の夫婦二人連れが多かった。

案内図や手持ちの地図で行く。ここからは頂上まで登り、そのあとは同じ道を戻るようだ。




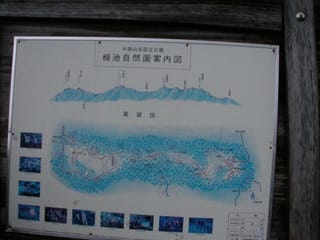
ここらあたりは尾根になっていて、足を踏み外すと危ない。一番高い所だが、見晴らしはよくない。


平地に到着。「浮き島湿原」水に浸食され、浮き島ができている。


行きのトイレに着く。


風穴。涼しい風が来る。温度計があり7度だった。


遥かに見える山の滝。


良く見かける。イワショウブ　岩菖蒲　らしい・・・。



やっと自然園の入り口に帰って来た。ロープウェイの時刻に間に合うが、次のを待つことに。栂池ヒュッテの食堂で
ブルーベリーアイスクリームをいただく。300円

シャーベット感覚でおいしかった。

ロープウェイの駅入り口



ロープウェイのロープが展示してあった。


確か、２時２０分発に乗り、３時半頃にはホテルに帰ったかな。



このあと、ゴンドラ乗り場近くの温泉「栂の湯」に行く。ホテルのフロントで割引券を購入。600円。
「栂の湯」は売店の２階にある。１階売店はゴンドラの客を対象としたお土産が主体。




　温泉は、透明なアルカリ泉で、ホテルと同じ。脱衣所は鍵なしのロッカーだが、貴重品ロッカーもあった。100円かかる。100円玉は戻らないやつだった。
　温泉には客はいなかった。一人でゆっくりと風呂に入る。サウナもあり、３回ぐらい入ったか・・・。サウナの中には時計がなく、砂時計の５分計があった。

　　
ずっと奥が露天風呂だが、天井もあり、露天という感じではなかった。

　脱衣所には体重計があったが、アナログのもの。デジタルのしっかりしたものがあるといいのだが。冷水機などもなく、もう少し施設が充実していないと客が入らないな、と思った。
　休憩室は都会の銭湯のような程度。少し広かったが、冷たい飲み物の販売があった。ビールがないのが残念。


　１階の売店でビールを買って一息入れた。

　このあとホテル前のコンビにでビールを購入。500mlのもの350円。ホテルだと400円。
夕食


デザート


このあとホテルの風呂に入り、２日目は終わり。

数学３ 第３章「微分法」 終わり

　だいぶ前に数学３の第３章「微分法」が終わった。
　ここでの発見は、sin とcosの微分法。

　たいていの教科書では、sin xの微分は微分商((sin (x+h)-sin x)/hの分子は
（三角関数の和差）→（三角関数の積）の公式を使って、sin(x+h)-sin x=2cos(x+h/2)sin h/2と変形しているが、

　この教科書ではそのまま
　　sin(x+h)-sin x=sin x cos h+cos x sin h -sin x=cos x sin h-sin x(1-cos h)と変形。
　微分商は　(cos x sin h-sin x(1-cos h))/h
　この場合は sin h/h と (1-cos h)/hの２つの極限値を使う。それぞれが極限値を持つということに触れ、極限の操作を分ける。
　すなわち、cos x sin h/hと-sin x(1-cos h)/hそれぞれの極限値の和から、(sin x)'=cos x を得る。

　どちらの方がいいのだろうか。どうしてこの教科書のやり方は少ないのか、ここら辺りは高校の先生方に聞いてみたいと思った。

　もうひとつ、以前、「大学の編入試験を受けたいので数学について教えて欲しい」との教え子の連絡で、編入試験用の問題集を購入した。そこには、「対数微分法」が紹介されていた。こんなのあったかなーと思い、大学の教科書で調べてみると、高校の復習のところに載っていた。　というわけで、受験勉強をしていたころの教科書を調べてみたら、数学３に確かにあった。だが、私は受験時代この手法を知らなかった。「新課程」の内容だったのだが、予備校でも習っていなかったと思う。よくまあ、大学に受かったものだと思った。

　さて、数学３の第３章が終わったので次は数学Cの第３章、確率分布とやらの章に入る。苦手なところを復習することになる。