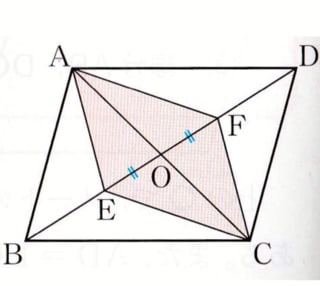
図で平行四辺形ABCDの対角線ACとBDの交点をOとし、
対角線BD上に点E,FをOE=OFとなるようにとる。
このとき、四角形AECFは平行四辺形になる。
このことを証明しなさい。
この問題の証明は次だが、これが生徒には分かりにくい。
=========================================================
平行四辺形の対角線はそれぞれの中点で交わるので、
OA=OC・・・(1)
仮定から
OE=OF・・・(2)
(1),(2) から
対角線がそれぞれの中点で交わるから、
四角形AECFは平行四辺形である。
証明終わり
=========================================================
この証明、似通った文章をよく読んでみると
「平行四辺形の対角線はそれぞれの中点で交わるので、」
「対角線がそれぞれの中点で交わるから、」
の「は」と「が」に注目してみる。
証明を次のように改良してみた。「四角形の」という言葉を入れただけだが、
少し分かりやすくなる。
====改良版=====================================================
平行四辺形の対角線はそれぞれの中点で交わるので、
OA=OC・・・(1)
仮定から
OE=OF・・・(2)
(1),(2) から
四角形の対角線がそれぞれの中点で交わるから、
四角形AECFは平行四辺形である。
証明終わり
=============================================================
つづく

















