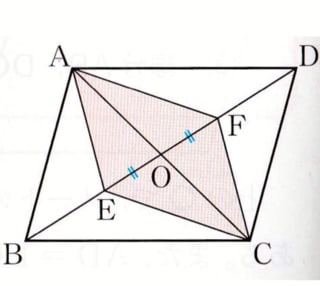
図で平行四辺形ABCDの対角線ACとBDの交点をOとし、
対角線BD上に点E,FをOE=OFとなるようにとる。
このとき、四角形AECFは平行四辺形になる。
このことを証明しなさい。
再びもとの証明を見てみよう。
===元の証明==========================================
平行四辺形の対角線はそれぞれの中点で交わるので、
OA=OC・・・(1)
仮定から
OE=OF・・・(2)
(1),(2) から
対角線がそれぞれの中点で交わるから、
四角形AECFは平行四辺形である。
証明終わり
======================================================
元の証明は
「対角線はそれぞれの中点で交わる」
「対角線がそれぞれの中点で交わる」
と二つの似通った文章があり、この違いが分からないと、この証明は理解出来ない。
この違いは「は」と「が」の使い方に秘密がある。
「対角線はそれぞれの中点で交わる」で使われた「は」のあとには
「中点で交わることを具体的に示したことがら」すなわち「OA=OC」が記述される。
これに対して
「対角線がそれぞれの中点で交わる」で使われた「が」については、その前に
「中点で交わることを具体的に示したことがら」すなわち「OE=OF」が記述され、
この事実を受けて、
「対角線がそれぞれの中点で交わる」のあとに
「四角形AECFは平行四辺形である。」ということがらを述べている。
「は」を使うときは、そのあとに具体的な記述が来る。
「が」を使うときは前の記述を受けて、新しいことを述べている。
このことの具体例を見てみよう。
つづく
つづく
















