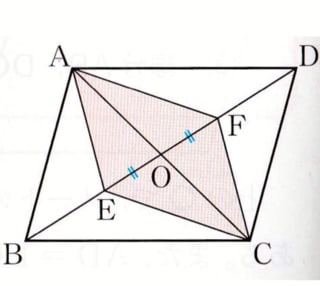
図で平行四辺形ABCDの対角線ACとBDの交点をOとし、
対角線BD上に点E,FをOE=OFとなるようにとる。
このとき、四角形AECFは平行四辺形になる。
このことを証明しなさい。
===元の証明==========================================
平行四辺形の対角線はそれぞれの中点で交わるので、
OA=OC・・・(1)
仮定から
OE=OF・・・(2)
(1),(2) から
対角線がそれぞれの中点で交わるから、
四角形AECFは平行四辺形である。
証明終わり
======================================================
「は」と「が」について
「対角線はそれぞれの中点で交わる」で使われた「は」のあとには
「中点で交わることを具体的に示したことがら」すなわち「OA=OC」が記述される。
これに対して
「対角線がそれぞれの中点で交わる」で使われた「が」については、その前に
「中点で交わることを具体的に示したことがら」すなわち「OE=OF」が記述され、
この事実を受けて、
「対角線がそれぞれの中点で交わる」のあとに
「四角形AECFは平行四辺形である。」ということがらを述べている。
「は」を使うときは、そのあとに具体的な記述が来る。
「が」を使うときは前の記述を受けて、新しいことを述べている。
このことの具体例を見てみよう。
「は」の例
三角形の内角の和は180度だから
平行線の錯角は等しいから
合同な図形の対応する辺の長さは等しいから
どうだろうか、こう言われると「から」のあとには、具体的な辺や角が
等しいということを表す式が記述されだろうことが容易に想像される。
「が」の例
2組の辺とその間の角が等しいから
錯角が等しいから
2組の対辺がそれぞれ等しいから
こう言われると「から」のあとはそれぞれ
2つの三角形は合同である。
2直線は平行である
平行四辺形である
という新しい事柄が記述されるだろう。
「は」を使うときはそのあとにそのことを表す具体的な記述が来る。
「が」を使うときはその前の事柄を受けて、新しいことを言う。
ところで「は」も「が」も主語に付く「格助詞」である。
「助詞」のない英語ではどう表すのだろうか、と疑問を持ったので、
大学教授であった友人に聞いてみた。
つづく

















