これまでの復習。

を証明しよう。
==============================================
まず (1)

とおく。
この級数はn個の項を持つ。
項数を2倍にすると (2)
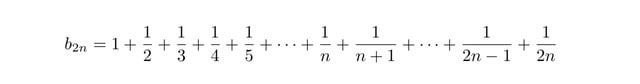
(1)を2で割ると、分母が偶数だけの級数が出来る。(3)

(2)から(3)を引くと、分母が奇数だけの級数が出来る。項の個数はn個であることに注意する。

ここからもう一度(3)を引くと、分母が奇数の正の項と分母が偶数の負の項で作られた級数が出来る。
項の個数は2n個であることに注意する。

もうひと息。

ここから、式の工夫をする。
(1)からlog n を引いた式で n→♾ とすると、この式は γ に収束する。
(「極限の勉強 級数3」を参照)
同様に(2)から log(2n) を引いた式もやはりγに収束する。
そして、log(2n) = log 2 + log n. であった。
これがヒントだが、詳しい説明は後日。
級数5へつづく

















