面白そうな本

とりあえず何か表示したり動かしたりっていうのは
これまでにも何かしら作ってきたんだけど、なんかこう、
表示するところまでで終わりって感じで、もうちょっと
複雑なものをマイコンで組んでみたいって思いが
あったんだけど、そんなオイラにちょっと面白そうな
本発見。

その１。コンピュータ麻雀のアルゴリズム
その２。コンピュータ将棋のアルゴリズム
その３。リバーシのアルゴリズム C++&Java対応

３冊ともＩ／Ｏブックス。うーん、一気に読んでみたい。

そういえば、学生時代に提出課題で何かちゃんとしたもの
作って出さないといけなかったんで、人対コンピュータの
対戦リバーシ（人対人も可）っていうのを組んだんだけど、
あれは盤の１マス１マスに有利／不利の重み付けを置いた
だけのロジックだったから、序盤は強くて後半はメチャメチャ
弱い…って代物だった。

それよりも、当時からどうしても組んでみたいものの一つ
が麻雀系のゲーム。うん。今更組んでみたところで
どうってこと無いんだけど、なんとなく遣り残した
宿題っていうか…。
ちゃんとした麻雀じゃなくて、当時別冊ヤンマガの
付録についてたぎゅあんぶらー自己中心派の寿司麻雀。
アレを組んでみたいんだよな…。

ＦＭ－７にはプログラムが公開されてたような気がする
んだけど、オイラの８８シリーズでは出てこなかった…

その残尿管もあり、なんとなくマージャン系のゲームが
組んでみたいんだな。

どうせなら、この手の中身がちゃんとしたものを一度
組んでみたいんだよな。

ＢＰＦ

エレウケの妄想がだいぶ現実化するところまで見えて
来たんだけど、この続きは実際にモノを組み立てたり
アセンブラでプログラム組んだり、実験用のドライバボード
を作ったりしないと進められない…当面はそこまで手が
つけられる暇が無さそうなので、もうひとつ別の実験の方に…。


この間のＬＴｓｐｉｃｅでやってたＢＰＦの実験の方。
↓この実験ね。

オペアンプのＢＰＦで１０ＫＨｚとか２０ＫＨｚとかだけ
を拾って、ダイオードで検波するってだけの回路。

コイツを使って何をするかって言うと…
↓この続き。
http://brown.ap.teacup.com/nekosan0/115.html

そう。マイコンでバーコードを読みたい。バーコード
リーダを作りたいって訳。

ポイントになるのは、外乱光の中からバーコードで
反射した光だけ読み取って、外乱光は読み取らない
ための変調／復調回路。
そして、あの細ーいバーコードの情報を正確に読み出す
ための光学ピックアップの構造。
あとは各種バーコードのコード／デコードフォーマット。

フォーマットは
http://www.n-barcode.com/
ここが詳しいので、色々ある中から面白そうなものを
拾ってくるとして、変調／復調も回路の目処が
なんとなく立った感。

残る課題は光学ピックアップの部分。まずは妄想を練る。

受光素子としては、とりあえず可視光線が使いやすそう
だから可視光（緑ＬＥＤを想定）をセンシングできる
センサーとして、
http://akizukidenshi.com/catalog/g/gI-02325/
これなら数十ＫＨｚまでは追従しそうなので、
この間既に買い置きあり。それ使う予定。

本当は、赤外線ならリモコン用のセンサーが使いやすい
はずなんだけど、秋月とかで買える赤外線センサーは
変調が３８Ｋｈｚ固定だし、発色的にも目で見てどこを
センシングしているのか解り難いのが難点。
なので可視光線をわざわざ選んでいる訳。

さて、これを光学的に細い線を正確に読み取る仕組みが
必要になるんだけど、方針としては大きくは2つの案。

（１）レンズを使ってバーコードの拡大像を作り、
　　　その像をセンサーで読み取らせる

（２）小さな箱の一部分に小さな穴を空け、その
　　　箱の中にセンサーを埋め込み、穴をバーコード
　　　に近づけてスッと移動させて読み取る

といった感じ。何と言っても細いので、どちらにしても
加工精度が大変っぽいのと、外乱光に対して信号の光
が微弱なので変調は必須。

ＣＣＤみたいに1画素が凄く小さいといいんだけど、
ＣＣＤ1画素だけ…みたいな都合のいいデバイスは
売ってないみたいなので、既製品のセンサーを
使って作らないといけないんだなぁ。

一つの案としては、シャーペンの先っぽ…０．５ｍｍとか
の穴が空いてる円錐形の部分…を取り外して、その中に
センサーを入れちゃうって案。
もしくは上記の通り小さな箱の隅っこに剃刀とかで極小さな
穴を空け、バーコードの前をスッと横切って読み取る方法。

これらなら複雑な光学系は要らないので何だかんだで楽そう
な気がするんだけど、分解能がどれだけ細かいのやら…
何しろ「ピンホールカメラ」そのままの原理だから。

もう一つはやはりレンズで数倍に拡大した像を作り、
その像の焦点のところに（やはり小さな窓を開けた
状態の）光センサーを置いてあげれば結構細かい
ところまで読み出せるはず。なにしろ昨今のデジカメ
とやってることはいっしょだから。

できれば前者で何とかならんかなぁ？って思って
居るんだけど、さすがにバーコードの細かさを
ピンホールカメラで読み取るのは厳しいかなぁ…

でも「とりあえず実験してみる」だけならやっぱ
ピンホールカメラ式の方が手っ取り早いからな。
それでダメならレンズ式って構え方かな。

レンズはレンズで秋月で大量に買い込んであるから、
いざと言う時にはそれ使おう。
とりあえず手を動かして、実験材料を揃えておきたい
ところ。

ようやくエレウケのピックアップ実験

去年からずーーーーーーと引っ張りつづけている実験の
一環。以前作ったこのソリッドウクレレ↓




コイツにおいら謹製のエレウケ専用ピックアップ（試作）
を取り付けて、ＦＦＴを掛けてみようって寸法。
まぁ、ＦＦＴのアセンブラ用ライブラリはまだ未着手
なので、使うのは秋月で買ってきたｐｉｃｏ　ｓｃｏｐｅだけど。

で、実際に弾いてみた波形はというと…

まずは４弦＝Ｇの音。


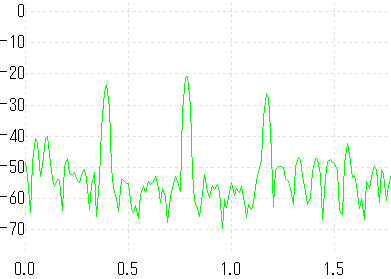
うん。おおよそ「基音」＋「整数倍音」の構成になってて
ｇｏｏｄ！

他の弦も大体同じ。以下それぞれ３弦（Ｃ）、２弦（Ｅ）、１弦（Ａ）





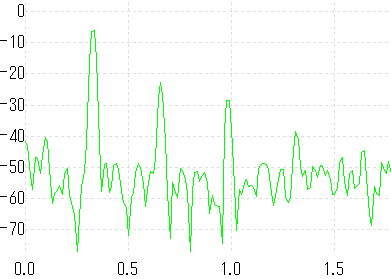
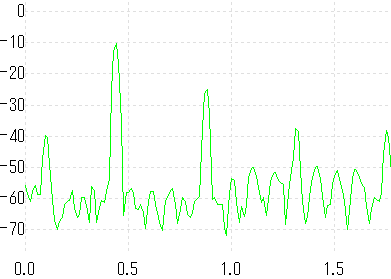
…うん。大体イイカンジ。
Ｇの音が基音より倍音のほうがちょっと大きい感じなのが
気になるところだけど、まぁその辺は実験の条件にも
因る気がするし、いざとなればソフト処理でなんとか
できるでしょ。

今回は、ピックアップのアンプ回路にNJM072を使っちゃった
ので、前回と単純比較はできないんだけど、まぁだいたい
ｏｋでしょう。ねらい通り。


さて、周波数成分じゃなくて”実際の波形”はと言うと…

まずは弦を弾いた直後の波形。

こんな風に、サリーちゃんのパパが横にたくさん並んで
いる状態。
弾いた直後は倍音成分（整数倍音、非整数倍音）がいっぱい
出ているんだと思うんだけど、何回弾いても大体こんな波形。
こんなもんなの？

弾いてからワンテンポ遅らせたところの波形は…

こんな風にサリーちゃんのパパの髪型が丸くなって…

もうちょっと経つと


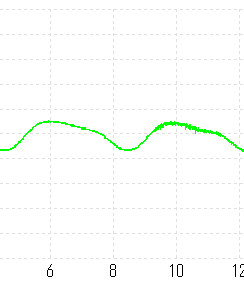
こんな風に海ボウズに変わってく感じ。


正弦波に近づいていく感じと考えると、倍音成分が
先に抜けてって、明るい音から丸い音に変わっていく
感じと捉えればいいのかな…


さて、波形や周波数成分のグラフを眺めてニマニマ
したいわけじゃなくて、何しろタイムラグが問題なのが
電子楽器。そのへんに関する懸念事項洗い出しってわけ。

タイムラグを生じさせる原因として考えられることは…

（１）ｍｉｄｉ音源自体のレスポンス
（２）ＦＦＴ入力用の全サンプルをＡＤ変換完了までの時間
（３）ＦＦＴの処理時間
（４）弦の振動のうち基音成分が安定するまでの時間

このうち、今回の波形で見てみたかったのは（４）に
関すること。
実物のウクレレなら、弾いた直後の複雑な倍音成分
（含む：非整数倍音）も音として耳に届く訳だけど、
エレウケというとＦＦＴ掛けて周波数成分を抜き出して、
さらにそこからｍｉｄｉ信号を生成して、ｍｉｄｉ音源側で
またアタマから音を創り出す処理を行う…みたいな処理を
やらないといけないので、どうしてもタイムラグは
避け様が無いわけ。

特に、サリーちゃんのパパ状態の時にどんな周波数成分
が混じるのか、基音だけが旨く取り出せるのか。そこが
見えればある程度目処が立つんじゃないかと。

で、やってみた感想ですが…なるようにしかならない…
かな。

そんなもんです。


あとは、実際にアセンブラ用ライブラリとそれをドライブ
するテストプログラムを適当に組み上げてみて、色々な
条件設定して、実機テストやってみてから考えよう…


まぁ、ちゃんと倍音成分が分離できるって判っただけで
安心したな。目下のところ、めでたしめでたし。

開平法

開平法について調べてみたら、wikipediaに載ってた。
http://ja.wikipedia.org/wiki/%E9%96%8B%E5%B9%B3%E6%B3%95

一通り眺めてみて、詳細までは理解できてないけど、
筆算で開平を行う処理方法はまぁ解った。なるほど。

で、じゃぁこの筆算の方法を使って開平を行おうか
って考えてみると、結構ややこしそうで足踏み。
特にアセンブラだと…めんどくさそう…

ってことで、昨日考えた方法の方がプログラムを組む
には簡単そうな気がするし、何より速そうだから、
自分で組むとしたらまずは自前の方式かな。表計算ソフト
で一応処理方法の妥当性はある程度見えたし。
残るは精度の問題だけ。

この平方根の開平処理を含め、ＦＦＴのアセンブラライブラリ
として、64点、128点、256点あたりを用意しておけば、AVRの
megaシリーズの登載メモリを加味した用途なら、今後の
アンナコトやコンナコトにも事足りるのではないかと。

まずは汎用できるライブラリをちょっとずつ組み上げて
いこう。組み上げたら色々信号を取り込んで実験してみよう。


ふと思い付いて実験。オイラの愛機ペンタックスｋ－７。
当然一眼「レフ」なので、レフ＝反射用のミラーが入ってて、
シャッター切るとミラーがパタパタするんだけど、
いわゆるtime lapseっていう類いの撮影をやるときに
ミラーがパタパタして困っちゃう訳。三脚を振動
させちゃったりとか。あと耐久面も。

で、ふと思ったんだけど、ライブビュー機能を使えば
ミラー上がりっぱなしで連写できるはずだろう…、と。

で、実験してみた。

…当然うまく行くわけ。で、撮った写真（ｊｐｅｇ）を
ムービーツールで結合してみると、旨い具合にちゃんと
time lapse的な写真になっている…。シメシメ。
ちょっと困っちゃうのは露出制御のことだな。ＡＥまかせ
にしておくと、ムービーに繋いだ時に不自然に輝度が
変化しちゃうんでは？と。

あとまぁ、ミラーはパタパタ言わないんだけど、当然
フォーカルプレーンシャッターが行ったり来たりする
のは避けられないので、どうしてもそのメカ部分の寿命
はちょっと心配になるんだけど…

そもそもムービーで撮っておいてから高速再生用に編集
したほうがいいのか、１枚１枚写真で撮ってから結合
したほうがいいのか。

ライブビューなんて、あまり使う予定も無かった機能なんだ
けど、あったらあったで便利なのかもしれないな。
ミラーレスのレンズ交換式カメラが欲しかった理由の一つ
はこのtime lapse撮影だったから、これだけはＫ－７だけ
でもいいかもしれない。

この手の撮影は、むしろマニュアル露出やマニュアル
フォーカス、レリーズが使えるコンパクトカメラの方が
やっぱ向いてる気がするな。


自転車でお買い物＆夕食。スーパーのフードコートで
飯食って、買い物済ませて自転車置き場に戻る。来る時に、
リヤタイヤだけ空気が甘くなってたから、駐輪場にあった
無料の空気入れを借りて空気を入れて帰ろうと思ったん
だけど…

空気入れてみたら、空気が「ブシューーーーー」って出ちゃう。
何度やっても出ちゃう。うーん、虫ゴムか？

虫ゴムを取り出してみてみると、先っぽのチューブが
吹っ飛んでる。空気漏れ防止用のリングゴムも劣化してる。
うーん、結構最近交換したばっかだと思ったんだけどな…。

スーパーの入り口に自転車売り場があったので、早速
虫ゴムを交換してもらうとバッチリ回復。おいらは
スーパーバルブの方が好きなんだけどな。
今回寿命になっちゃったリヤタイヤは確か普通の虫ゴム、
フロントタイヤだけスーパーバルブ。なんかの時に
フロントだけスーパーバルブに替えたんだけど、
リヤは替える機会が無かったな。今度替えておこう。

思いついた。

一昨日以来の悩み。アセンブラで平方根の解法をコンパクトに
行う方法。色々考えて見たところ、よさげなのを思いついた。

平方根といえば、まずはニュートン法。1箇所適当な初期値
を与えて、そこから漸化式で近づけていく方法。これは
計算が面倒だし、割り算（しかも割るほうの数が変数）が
出てくるし、収束条件を考えるのも大変だし…


というわけで、別の方法が無いかな…と。
そもそも平方根って何よ？って考えると、０．５乗するわけ。
それを旨く利用できないか数理的に攻めてみる。
しかも、今回は16ビット幅のデータを開平して、8ビット幅
の整数データを取り出せれば十分だから、精度はせいぜい
その範囲。そのあたりの条件を旨く適用しちゃう。

まずａという変数（とりあえず0～65535の16ビット幅）を
2進数の浮動小数表示にしてみるところから。

　ａ＝ｎ×２＾ｍ

固定小数表示のａを浮動小数表示のｎ×２＾ｍという形で
表してみたわけ。
ここでｎは仮数部、ｍは指数部とします。ｎは8ビット幅
精度の数値に丸めちゃう。←実はこれポイント。
2進数だから、ａを適宜右にシフトしたのがｎに、シフト
した回数がｍに入るだけ。ここは処理的には単純。

で、両辺平方根を取ると

　ｓｑｒｔ（ａ）＝ａ＾0.5＝（ｎ×２＾ｍ）＾0.5

となるので、整理すると

　＝ｎ＾0.5　×　２＾（ｍ/2）

となるわけ。ｍがもし偶数ならこの右半分はシフト命令
の組み合わせだけで組めちゃう。奇数なら、最後に
定数の１．４１４…（＝ｓｑｒｔ（２））を掛ければｏｋ。
ってことでここはシフト命令とハードウェア乗算器だけで
組めることが判っちゃう。

で、問題は残った部分のｎ＾0.5の部分。結局平方根が
出てきちゃうジャン！って言うのは早計。上述の通り
ｎは8ビット幅に丸めちゃってるので、実際に取り得る
数値は128個から多くても256個のはず。
（個数は処理ロジック次第）

この程度の定数テーブル、しかも1個1バイトしかないことを
考えると、128～256バイト程度。十分収まる範囲。バッチリ！
16ビット幅だと65536個の定数テーブルになっちゃうのと
比べれば月とすっぽん。

あとは、ｍが偶数なら
　　ｓｑｒｔ（ｎ）×２＾（ｍ/2）
を、奇数なら
　　ｓｑｒｔ（ｎ）×２＾（（ｍ-1）/2）×１．４１４…
を計算すれば良い訳。これらすべて平方根の定数テーブル、
シフト演算、ハードウェア乗算という処理速度の速い命令
だけで済んじゃうはず。

あとは計算途中で精度を下げたりしてることの影響度合い
だな…ってことで表計算ソフトでシミュレーション。

試しに、適当に作り出した数値を元に平方根の計算を
やってみると…

0001001010110100b （10進数で4788）は、平方根を取ると
69.195となるので、小数点以下四捨五入すると69。
これが求まればゴール。

さて、表計算上でシミュレーションをしてみると…

まずｎですが、アタマの0三つを取り除いてから8桁取り出し、
ついでに9桁目が1なので四捨五入で繰り上げておくと、
ｎ＝10010110bとなります。本来は仮数部は左端の1が
1の位になるんだけど、モロモロ端折る都合で今回はこの
8ビットデータを全部小数点以上の位としてしまいます。
すると指数ｍはこの場合5。つまり切り捨てた部分の桁数が
2進数で5桁（5ビット）分。
整理すると、
　　ａ＝10010110×２＾5
　　　　　ｎ＝10010110
　　　　　ｍ＝5
というわけ。数学的には美しくないけど、おいらは数学者
じゃないのでこれはこれで良しとしちゃいます。

で、この場合のｎは10進数でいうと150。
１５０を定数テーブルでサーチしたつもりになって
電卓で平方根取ると12.247…となるので、まるめて
１２と仮定することにします。

さて、ａ（＝4788）の平方根はというと、さっきの式を使って
　ｓｑｒｔ（150）×２＾((5-1)/2) ×1.414…
　＝　12 ×　２＾2　×　１．４１４…
　≒　68

…うーん、微妙に惜しい感じだけど、まぁこのくらい
まで求まればいいんじゃない？一番大きい誤差は150の
平方根が12って仮定しているところだな。ここはちょっと
誤差がでかすぎる…。

その辺も含めて整理しなおせば、16ビット数値の平方根を
求めて8ビット幅で返す処理はまぁまぁ実用レベルの精度
かつ速い処理速度（皮算用では100クロック～200クロック
程度？）に収まるんじゃないかと。

今回参考にしたページを。↓
http://d.hatena.ne.jp/Koonies/mobile?date=20090715&section=sqrt
ありがとうございました。


そういえば、ＣｈａＮさんの所に便利なライブラリが
載ってたな…と思って見てみる。
http://elm-chan.org/cc.html

16ビット幅の平方根はおいらが考えた方法よりもっと
メモリ効率よくできてるみたい。うーん、どんなロジック
で開平してるんだろう？