新しい出生前診断の陽性的中率は予想外に低い

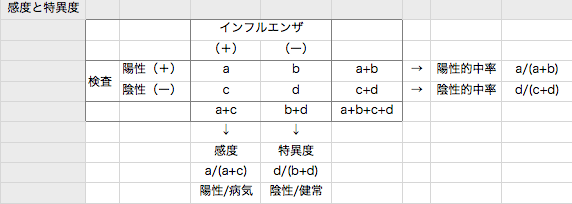
インフルエンザ検査の陽性的中率・陰性的中率を式とグラフを示しながら説明しました。
同じ理屈で、いま問題となっているお母さんの採血だけで診断できる「新しい出生前診断」について考えてみることができます。

感度 sensitivity　s　
特異度 specificity　p
有病率　x
陽性的中率 = sx/(sx + (1-p)(1-x))
陰性的中率 = p(1-x)/((1-s)x + p(1-x))

これをエクセルのシートに入れてみれば簡単に出て来ます。
この結果については、すでにこちらのブログで紹介されています。

遺伝のはなし#11：トピック「新しい出生前診断」
September 11 [Tue], 2012, 20:00
http://yaplog.jp/ohgimachi2511/archive/309

問題は有病率の低さからくる陽性的中率の意外なほどの低さです。
上記ブログからその部分を引用してみます。

--------------------------------------------------------------------------------------
今話題の出生前診断、マスコミがいう精度とは感度・特異度が約99％(実際は感度98.6％, 特異度99.8％)ということ。
たしかにこの数字だけを見れば、すごい検査のようみえるけど例えば35歳の妊婦がこの検査で陽性だとしても、事前確率(ダウン症候群の罹患率)は約1/300だから、陽性的中率は62％にすぎない（つまり検査陽性でも1/3は実際にはダウン症候群ではない）。
同様に40歳で事前確率1/100として陽性的中率は83％。これでも1/6は偽陽性ということになる。
--------------------------------------------------------------------------------------

Wikipediaには「21トリソミーの感度が99.1%、特異度が99.9%」と記載されていますが、ここではそのまま感度98.6％,、特異度99.8％を用いておきます。

感度 sensitivity　s = 0.986
特異度 specificity　p = 0.998

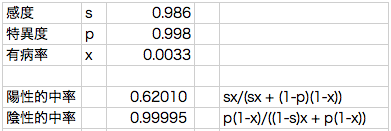
35歳
有病率　x = 0.0033
陽性的中率 = 0.62010（62.0%）
陰性的中率 = 0.99995（100.0%）



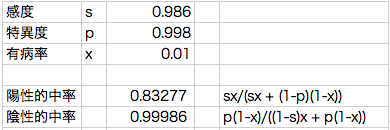
40歳
有病率　x = 0.01
陽性的中率 = 0.83277（83.3%）
陰性的中率 = 0.99986（100.0%）



計算結果は上記のブログに紹介されている通りの値で、検査結果が陰性であれば（検査が正しく行われているなら）まず間違いなく違うと言うことができます。

一方、陽性的中率は35歳で62%、40歳でも83%であり、偽陽性がそれぞれ38%、17%も出てしまう。
それよりも若い年齢に無闇に適用すれば、陽性的中率は更に低下してしまう。

このため、日本産科婦人科学会の指針案でも「35歳以上の高齢妊娠や超音波検査などで胎児に染色体異常が疑われる妊婦に限る」としているようです。

インフルエンザ検査：陽性的中率は特異度が高ければ十分に高い＜グラフ＞

ついでなので陽性的中率のグラフもつくってみました。
（クリックで別ウィンドウに拡大）



曲線は、上から順に感度90%, 80%, 70%, 60%, 50%の場合。（特異度99%）

感度 sensitivity　s　
特異度 specificity　p
有病率　x
陽性的中率 y = sx/(sx + (1-p)(1-x))

ここでは前項と同じく特異度（非インフル患者で検査陰性になる割合）が99%と仮定していますが、偽陽性が出ることはその程度に非常に少ない（1/100）と考えて良いので、流行がある程度以上のレベルで続いていれば、感度（s）が低下しても陽性的中率（検査陽性ならインフルエンザだと言える確率）は十分に高いことがわかります。

要するに、検査陽性ならほぼインフルエンザと考えて間違いないと。

ただし、流行がほぼ終息して有病率が非常に低いレベルになってくると、陽性的中率は少しずつ低下し、検査をして陽性でもインフルエンザではない（偽陽性）患者の割合が増えてきてしまいます。

そのレベルの流行状況だと、検査自体をあまりしなくなって来るのですが、たまたま検査して陽性だったとしても真の陽性か偽陽性かの区別はつかないので、陽性なら全例インフルエンザとして治療することになります。

流行時はインフルエンザ検査陰性でもインフルエンザである可能性が高い＜式とグラフで説明します＞

いまだに「インフルエンザ検査で陰性だからインフルエンザじゃない」と説明している医者がいるようで、本当に困った問題です。

昨年も同じことを説明しましたが、
→インフルエンザ検査が陰性のときの判断が流行時と非流行時で
　大きく違う理由　＜数字で説明します＞　2012年02月13日

今回は式とグラフで説明してみます。
（実際にはこんな式やグラフがなくても症状・経過と顔をみれば判断はさほど難しくないはずなのですが…）

検査キットに「感度90％」と書いてあっても、流行状況（有病率）と受診のタイミング（感度低下）によって、特に流行のピーク時には「陰性的中率（検査陰性の時に本当にインフルエンザじゃない割合）」は大きく低下します。

結論はタイトルの通り「流行のピーク時はインフルエンザ検査陰性でもインフルエンザである可能性が高い」ということです。

理由は、この「陰性的中率」のグラフをご覧下さい。
（クリックで別ウィンドウに拡大）



x は有病率で、１だと受診患者全員がインフルエンザ。
y は陰性的中率（検査陰性の時に本当にインフルエンザじゃない割合） 1に近いほど良い

陰性的中率のグラフは、こんなカーブになります。
曲線は、上から順に感度90%, 80%, 70%, 60%, 50%の場合。（特異度99%）
どの曲線も、有病率が大きくなるにつれて低下することが一目でわかります。

（式は一番下に書きますが）
特異度（p）を0.99で固定して、
感度（s）と有病率（x）を動かしてみると

流行時（有病率90%）

感度s=0.9　有病率x=0.9　陰性的中率=0.524
感度s=0.6　有病率x=0.9　陰性的中率=0.216

流行がピーク越え（有病率50%）

感度s=0.9　有病率x=0.5　陰性的中率=0.908
感度s=0.6　有病率x=0.5　陰性的中率=0.712

流行が下火（有病率10%）

感度s=0.9　有病率x=0.1　陰性的中率=0.989
感度s=0.6　有病率x=0.1　陰性的中率=0.957

流行時（有病率90%）には感度90%であっても「検査陰性患者の半分はインフルエンザ」であり、実際には受診タイミングが早くて感度が相当低下するので、感度60%だとすると、検査陰性患者の８割は実際にはインフルエンザであることがわかります。
それぞれ、上のグラフでどこにプロットされるかお確かめ下さい。

ですから、その時点での流行状況（有病率）と感度（受診のタイミングや症状などから大まかに見当をつける）によって、検査陰性の時に「インフルエンザの可能性が高い」と言うか「可能性は低い」と説明するかは全く異なってくるのです。
実際には有病率や感度もファジーなので、どちらとクリアカットに判断できない場合も多い。

以下、式とグラフについて説明しますが、面倒ならここまででも結構です。



この表を「２×２分割表」と言います。

　　　　　疾患あり　疾患なし
検査陽性　　ａ　　　　ｂ
検査陰性　　ｃ　　　　ｄ

検査陽性・インフル（真陽性）　a
検査陽性・非インフル（偽陽性）　b

検査陰性・インフル（偽陰性）　c
検査陰性・非インフル（真陰性）　d

感度 sensitivity　インフル患者で検査陽性になる割合
　s = a/(a+c)　
特異度 specificity　非インフル患者で検査陰性になる割合
　p = d/(b+d)
有病率　全患者中のインフル患者の割合
　x = (a+c)/(a+b+c+d)

＜↓計算経過↓＞　ここは飛ばしても構いません

全患者数　Q = a+b+c+d
インフル　a+c = xQ
非インフル　b+d = (1-x)Q

検査陽性・インフル　a = sxQ
検査陰性・インフル　c = (1-s)xQ

検査陽性・非インフル　b = (1-p)(1-x)Q
検査陰性・非インフル　d = p(1-x)Q

＜↑計算経過↑＞　ここまで

以上を代入すると次のような式になります。

陽性的中率（検査陽性のときに疾患である確率）
= a/(a+b)
= sx/(sx + (1-p)(1-x))

陰性的中率（検査陰性のときに疾患でない確率）
= d/(c+d)
= p(1-x)/((1-s)x + p(1-x))

（ここで、上のグラフに戻る）