立体幾何への動機３

以前の記事
====================================================
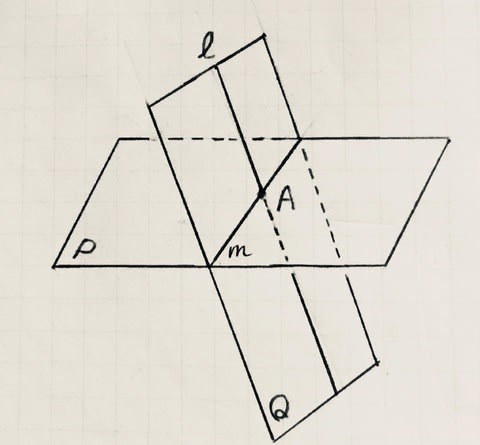
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。


直観的には明らかなのだが、はたしてそうなのか、
というと不安になる。
そこで証明しようということに。証明は背理法を使う。ここ
==========================================================

これの背理法を使わない証明を考えた。

証明
　点Aは直線Iに含まれるから、平面Qに含まれる。
　また、点Aは平面Pとの交点であるから平面Pにも含まれる。
したがって、点Aは平面Pにも平面Qにも含まれる。
公理により、２平面は一つの点だけを共有しないので、２平面
に含まれる点Aは平面PとQの交線mに含まれる。
点Aは直線lとmとの交点である。
　　　　　　　　　　(証明終わり)

この証明は多少不十分なところがあると思う。

「公理により、２平面は一つの点だけを共有しないので、２平面
に含まれる点Aは平面PとQの交線mに含まれる。」
というところだ。この論理を通すためには背理法が必要となるだろう。
つまり、もし点Aが交線mに含まれないとすれば、、、である。

やはり背理法は強力だ。


埼玉県入試問題との関係では、
平面P→入試問題の面ABCD
直線l→入試問題のEQ
交線m→入試問題のBD
交点A→入試問題のI
にあたる。




入試の模範解答では
「EQはlを通る」と言っていた。これは中学校段階の直感による。
論理ではどうかということだ。

さらに、切り口の面がEBQDになるのかということも疑問としてあるのだが、
それにも挑戦したい。


つづく

庭の菜の花

庭の菜の花の見納め。せっせと世話をし、育ててくれた女房に感謝。


この後引き抜いて、跡にミニトマトを植えるそうだ。

LINE通話

４月１６日のこと。


２月８日に高校の友人から来たLINE通話を、
間違えて、前日の１５日に来たものと思い込み、通話のボタンを
押してしまった。
酔っていたのと、その友人のことを思い出していたところだったので、
23時に通話ボタンを押したのだ。

１６日朝、友人から電話があり、通話した。
本人はLINEに慣れていなくて、
「間違えて電話したかも知れない」と言っていたが、
あとから履歴を見たら、私が寝ぼけて夜中に通話ボタンを
押していたことが判った。
電話があったものと勘違いするとは、ボケたものだ。

間違え通話のおかげで、友人の様子も分かった。
自宅に篭りっきりだそうだ。
電話は私のミスだったと謝りを入れておいた。

久しぶりにクラリネット

４月１１日。
久しぶりに公園でクラリネット。


笛も。


クラリネットは新しく手に入れたマウスピースの試奏。
12000円のものが中古か新古品で4000円はお買い得。
マウスピースについては後日アップ予定。

立体幾何への動機２

埼玉県入試
===========================================================
埼玉県の数学、学校選択問題。レベルの高い学校の入試。最後の問題。
（文は少し変えてあります。)


立方体と正四角錐を合わせた立体。
PA=AB=2cm
この立体を点E, B, Dを通る平面で切ります。
この平面と辺PCの交点をQとするとき、
PQ : QC を途中の説明も書いて求めなさい。　７点
================================================================

この問題の解答の解説で疑問。
「ACとBDの交点をIとすると、EQはIを通る」という。

ここでは問題を簡単にするため、「EQはBDの中点Iを通る」
としておこう。これが疑問だった。


EQが点Iを通るのは直感では分かるが、どうして？
図を見ると、切り口の面EBQDは直線EQを含み、面ABCDとの交線が
BDとなっている。
そこで、
「直線が平面と交わる点はその直線を含むもう一つの面と、元の平面との交線上にある。」
つまり、
「直線と交線との交点である」
このことを論理で説明したかった。

図でいえば、
「EQと面ABCDの交点をIとすると、IはDB上の点である」
ということだ。

つづく

立体幾何への動機１

以前の記事
====================================================
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。


直観的には明らかなのだが、はたしてそうなのか、
というと不安になる。
そこで証明しようということに。
===========================================================

以前、こんなことを記事にした。
その動機は何だったかということを思い出した。
埼玉県の高校入試問題だった。

再度紹介しよう。

===========================================================
埼玉県の数学、学校選択問題。レベルの高い学校の入試。最後の問題。
（文は少し変えてあります。)


立方体と正四角錐を合わせた立体。
PA=AB=2cm
この立体を点E, B, Dを通る平面で切ります。
この平面と辺PCの交点をQとするとき、
PQ : QC を途中の説明も書いて求めなさい。　７点
================================================================

この問題の模範解答を見て、疑問を感じたのだ。

つづく

孫の子守り

４月１０日、孫の子守り。


勉強が終わり、公園に。


野球。


野球のあとはスーパーで買い物。
この日の昼食は、孫の希望でラーメン。

立体幾何の勉強に思う

「立体幾何のすすめ」という題で、2016年の３月に記事を書いたことがある。
探し出すことが出来た。
４年前だった。この記事のあとの立体幾何についての記事がない。
当時、勉強用にB5のノートに、これら２冊の本を交互に読みながら、
内容をまとめていた。
途中から、背理法を使った証明が分からなくなり挫折した。
ブログ記事も「立体幾何のすすめ１」と連載を謳っておきながら、
続きの記事がアップ出来なかった。
２冊を交互に読んだのが混乱の原因だったようだ。
今回は１冊に絞って、A4のルーズリーフにまとめてみた。
今のところ順調である。

気になったので再度記事を検索したところ、
さらに１年前の2015年にも２つの記事が見つかった。
「平面に垂直な直線について」
「立体幾何の勧め１」

記事に証明のリンク先があったが、リンク先不明になっていたので、
改めてリンク先を改訂しておいた。

「立体幾何の勧め１」も連載を謳っておきながら、挫折していた。
２度も挫折したのだと改めて反省。
今回はようやくうまく勉強が進んでいる。

コロナ疑惑

４月６日、孫との野球をし、昼食後昼寝。
この日はやや寒く、朝は７時起きで寝不足感があった。
孫たちが帰ってから、何もやる気がなく、
ダラダラと過ごしていた。
熱っぽいので体温を測ると３７度超え。やばい。
一時は37.7度にも。もしや。せき、喉の軽い痛み。
ちょうど２週間前にお囃子稽古の前に、錦糸町の
楽天地温泉に行ったり、居酒屋さんでホッピーを
飲んだりした。もしや、もしやだった。



そして、４月７日は一日中寝ていた。体力と免疫力を
温存だ。体温は３７度の前半を行ったり来たり。
コロナで入院するようなことになったら、いろいろ
片付けておかないといけないことがある。
と、夜もおちおち眠れず、４月８日。
体温はやっと３６度台の平熱に戻った。
テレビでは、女性の芸人さんがコロナに感染した
ニュース。一旦下がった体温がまた上昇した、などとの
報道に、ますます心配になる。
この日も念のため、のんびりと。昼寝の時はパジャマに
着替えて布団で寝た。髪の毛を触ると風邪をひいた時
のように、敏感になっていた。
そして、４月９日。症状はほとんど消えた。
孫の子守りで風邪をひいたのかも。まだ少し軽い咳と
喉の違和感があるが、少しホッとした。

立体幾何をめぐって

ガロアの理論の勉強が行き詰まった頃、
新聞に埼玉県公立高校入試の問題が紹介されていた。
学習教室で役立つだろうと思い、解いていた。
最後の問題は空間図形だった。
その頃、塾をやっている知人からLINEで空間図形の質問
が来た。応えているうちに必要と思い、空間図形や立体幾何
の復習をすることにした。
どうしてかというと、空間図形のいろいろな性質を使って
受験問題を解くのだが、性質はほとんど直感に頼ることが多い。
高校の数学の教科書にも、空間図形についてきちんと
述べられてはいない。
ということで、
一度あきらめた立体幾何を再度勉強することにした。
なぜあきらめたかというと、立体幾何の理論は
「背理法」のオンパレードで理解できないことが多かった。

もう一つの理由は、ガロア理論で証明がよく分からないまま
分かったつもりで証明を読み終えることが多かった。
それはなぜかというと、それぞれの定理の意味の理解が
不十分なのと、いくつかの定理の集まりで構成された
「ガロア理論の世界」の構造がつかめていなかったからだ。

空間図形の本を読んで理解出来なかったのも、
同じことなのではないか。
つまり、自分の中に「空間図形の世界」がきちんと構成されて
いなかったからだと思った。
背理法で証明が分かるためには、空間というものが、
しっかり分からないと、証明が心にストンと落ちないのだ。
同じことがガロア理論の理解でも言えるのではないか。
遠回りになるが、立体幾何の勉強はガロア理論の勉強にも
役立つだろう。そう考えた。

そして、もしかすると学習教室の生徒に、数学が分かるため
にも、この勉強は役立つかも知れないと思った。
「数学の世界」が生徒の中に構成されれば、理解は深まる。
数学の世界の構成法を生徒につかんでもらうにはどうすればよい
かが、立体幾何の勉強を通じて分かるのではと思っている。

長くなった。立体幾何の直感と理論構成などについては後日触れる。