2006年11月12日の記事を再編集。
「三角形はいくつできる?」
生徒「最後の1本で2個できるから、98個。」
「対角線の最後は97本目のこれ(99→97)を引くと、
何と両側に三角形ができます。
だから(100-3)+1で98個。」
「百角形の内角の和は?」
生徒「180度×98」
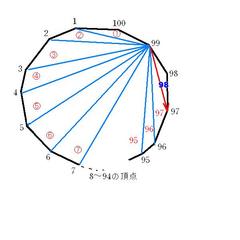
「では、百角形でなくて、n角形だったら?内角の和は?」
生徒「180度×(n-2)です。」
「その通り!実は100のところをnとすると99はn-1、98はn-2、
97はn-3となる(ここは生徒に考えさせれば良かった)」
「今と同じ理屈で、対角線は(n-3)本引けて、三角形は
n-3+1=n-2だから(n-2)個できますね。」
ではまとめましょう。「n角形の内角の和は180度×(n-2)」
(おしまい)
対角線で区切った時に出来る三角形の個数を用いて
多角形の内角の和=180度×(三角形の個数)
がどうして成り立つのかについての詰めの論議
はこの後に。
















