いまだに「インフルエンザ検査で陰性だからインフルエンザじゃない」と説明している医者がいるようで、本当に困った問題です。
昨年も同じことを説明しましたが、
→インフルエンザ検査が陰性のときの判断が流行時と非流行時で
大きく違う理由 <数字で説明します> 2012年02月13日
今回は式とグラフで説明してみます。
(実際にはこんな式やグラフがなくても症状・経過と顔をみれば判断はさほど難しくないはずなのですが…)
検査キットに「感度90%」と書いてあっても、流行状況(有病率)と受診のタイミング(感度低下)によって、特に流行のピーク時には「陰性的中率(検査陰性の時に本当にインフルエンザじゃない割合)」は大きく低下します。
結論はタイトルの通り「流行のピーク時はインフルエンザ検査陰性でもインフルエンザである可能性が高い」ということです。
理由は、この「陰性的中率」のグラフをご覧下さい。
(クリックで別ウィンドウに拡大)

x は有病率で、1だと受診患者全員がインフルエンザ。
y は陰性的中率(検査陰性の時に本当にインフルエンザじゃない割合) 1に近いほど良い
陰性的中率のグラフは、こんなカーブになります。
曲線は、上から順に感度90%, 80%, 70%, 60%, 50%の場合。(特異度99%)
どの曲線も、有病率が大きくなるにつれて低下することが一目でわかります。
(式は一番下に書きますが)
特異度(p)を0.99で固定して、
感度(s)と有病率(x)を動かしてみると
流行時(有病率90%)
感度s=0.9 有病率x=0.9 陰性的中率=0.524
感度s=0.6 有病率x=0.9 陰性的中率=0.216
流行がピーク越え(有病率50%)
感度s=0.9 有病率x=0.5 陰性的中率=0.908
感度s=0.6 有病率x=0.5 陰性的中率=0.712
流行が下火(有病率10%)
感度s=0.9 有病率x=0.1 陰性的中率=0.989
感度s=0.6 有病率x=0.1 陰性的中率=0.957
流行時(有病率90%)には感度90%であっても「検査陰性患者の半分はインフルエンザ」であり、実際には受診タイミングが早くて感度が相当低下するので、感度60%だとすると、検査陰性患者の8割は実際にはインフルエンザであることがわかります。
それぞれ、上のグラフでどこにプロットされるかお確かめ下さい。
ですから、その時点での流行状況(有病率)と感度(受診のタイミングや症状などから大まかに見当をつける)によって、検査陰性の時に「インフルエンザの可能性が高い」と言うか「可能性は低い」と説明するかは全く異なってくるのです。
実際には有病率や感度もファジーなので、どちらとクリアカットに判断できない場合も多い。
以下、式とグラフについて説明しますが、面倒ならここまででも結構です。
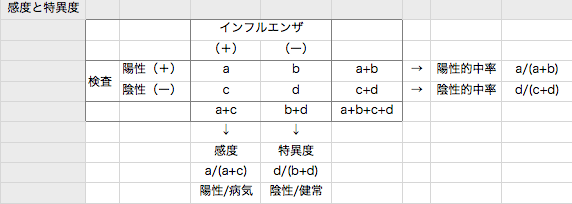
この表を「2×2分割表」と言います。
疾患あり 疾患なし
検査陽性 a b
検査陰性 c d
検査陽性・インフル(真陽性) a
検査陽性・非インフル(偽陽性) b
検査陰性・インフル(偽陰性) c
検査陰性・非インフル(真陰性) d
感度 sensitivity インフル患者で検査陽性になる割合
s = a/(a+c)
特異度 specificity 非インフル患者で検査陰性になる割合
p = d/(b+d)
有病率 全患者中のインフル患者の割合
x = (a+c)/(a+b+c+d)
<↓計算経過↓> ここは飛ばしても構いません
全患者数 Q = a+b+c+d
インフル a+c = xQ
非インフル b+d = (1-x)Q
検査陽性・インフル a = sxQ
検査陰性・インフル c = (1-s)xQ
検査陽性・非インフル b = (1-p)(1-x)Q
検査陰性・非インフル d = p(1-x)Q
<↑計算経過↑> ここまで
以上を代入すると次のような式になります。
陽性的中率(検査陽性のときに疾患である確率)
= a/(a+b)
= sx/(sx + (1-p)(1-x))
陰性的中率(検査陰性のときに疾患でない確率)
= d/(c+d)
= p(1-x)/((1-s)x + p(1-x))
(ここで、上のグラフに戻る)
昨年も同じことを説明しましたが、
→インフルエンザ検査が陰性のときの判断が流行時と非流行時で
大きく違う理由 <数字で説明します> 2012年02月13日
今回は式とグラフで説明してみます。
(実際にはこんな式やグラフがなくても症状・経過と顔をみれば判断はさほど難しくないはずなのですが…)
検査キットに「感度90%」と書いてあっても、流行状況(有病率)と受診のタイミング(感度低下)によって、特に流行のピーク時には「陰性的中率(検査陰性の時に本当にインフルエンザじゃない割合)」は大きく低下します。
結論はタイトルの通り「流行のピーク時はインフルエンザ検査陰性でもインフルエンザである可能性が高い」ということです。
理由は、この「陰性的中率」のグラフをご覧下さい。
(クリックで別ウィンドウに拡大)

x は有病率で、1だと受診患者全員がインフルエンザ。
y は陰性的中率(検査陰性の時に本当にインフルエンザじゃない割合) 1に近いほど良い
陰性的中率のグラフは、こんなカーブになります。
曲線は、上から順に感度90%, 80%, 70%, 60%, 50%の場合。(特異度99%)
どの曲線も、有病率が大きくなるにつれて低下することが一目でわかります。
(式は一番下に書きますが)
特異度(p)を0.99で固定して、
感度(s)と有病率(x)を動かしてみると
流行時(有病率90%)
感度s=0.9 有病率x=0.9 陰性的中率=0.524
感度s=0.6 有病率x=0.9 陰性的中率=0.216
流行がピーク越え(有病率50%)
感度s=0.9 有病率x=0.5 陰性的中率=0.908
感度s=0.6 有病率x=0.5 陰性的中率=0.712
流行が下火(有病率10%)
感度s=0.9 有病率x=0.1 陰性的中率=0.989
感度s=0.6 有病率x=0.1 陰性的中率=0.957
流行時(有病率90%)には感度90%であっても「検査陰性患者の半分はインフルエンザ」であり、実際には受診タイミングが早くて感度が相当低下するので、感度60%だとすると、検査陰性患者の8割は実際にはインフルエンザであることがわかります。
それぞれ、上のグラフでどこにプロットされるかお確かめ下さい。
ですから、その時点での流行状況(有病率)と感度(受診のタイミングや症状などから大まかに見当をつける)によって、検査陰性の時に「インフルエンザの可能性が高い」と言うか「可能性は低い」と説明するかは全く異なってくるのです。
実際には有病率や感度もファジーなので、どちらとクリアカットに判断できない場合も多い。
以下、式とグラフについて説明しますが、面倒ならここまででも結構です。

この表を「2×2分割表」と言います。
疾患あり 疾患なし
検査陽性 a b
検査陰性 c d
検査陽性・インフル(真陽性) a
検査陽性・非インフル(偽陽性) b
検査陰性・インフル(偽陰性) c
検査陰性・非インフル(真陰性) d
感度 sensitivity インフル患者で検査陽性になる割合
s = a/(a+c)
特異度 specificity 非インフル患者で検査陰性になる割合
p = d/(b+d)
有病率 全患者中のインフル患者の割合
x = (a+c)/(a+b+c+d)
<↓計算経過↓> ここは飛ばしても構いません
全患者数 Q = a+b+c+d
インフル a+c = xQ
非インフル b+d = (1-x)Q
検査陽性・インフル a = sxQ
検査陰性・インフル c = (1-s)xQ
検査陽性・非インフル b = (1-p)(1-x)Q
検査陰性・非インフル d = p(1-x)Q
<↑計算経過↑> ここまで
以上を代入すると次のような式になります。
陽性的中率(検査陽性のときに疾患である確率)
= a/(a+b)
= sx/(sx + (1-p)(1-x))
陰性的中率(検査陰性のときに疾患でない確率)
= d/(c+d)
= p(1-x)/((1-s)x + p(1-x))
(ここで、上のグラフに戻る)