インフルエンザ検査：陽性的中率は特異度が高ければ十分に高い＜グラフ＞

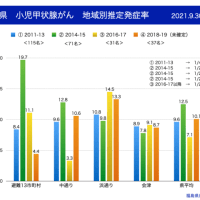
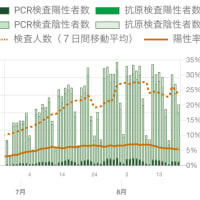
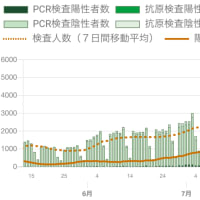
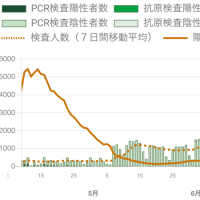
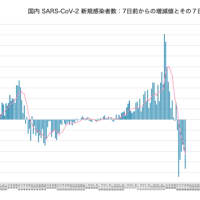
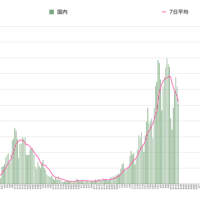
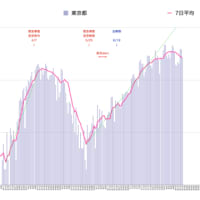
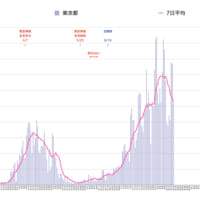
ついでなので陽性的中率のグラフもつくってみました。
（クリックで別ウィンドウに拡大）



曲線は、上から順に感度90%, 80%, 70%, 60%, 50%の場合。（特異度99%）

感度 sensitivity　s　
特異度 specificity　p
有病率　x
陽性的中率 y = sx/(sx + (1-p)(1-x))

ここでは前項と同じく特異度（非インフル患者で検査陰性になる割合）が99%と仮定していますが、偽陽性が出ることはその程度に非常に少ない（1/100）と考えて良いので、流行がある程度以上のレベルで続いていれば、感度（s）が低下しても陽性的中率（検査陽性ならインフルエンザだと言える確率）は十分に高いことがわかります。

要するに、検査陽性ならほぼインフルエンザと考えて間違いないと。

ただし、流行がほぼ終息して有病率が非常に低いレベルになってくると、陽性的中率は少しずつ低下し、検査をして陽性でもインフルエンザではない（偽陽性）患者の割合が増えてきてしまいます。

そのレベルの流行状況だと、検査自体をあまりしなくなって来るのですが、たまたま検査して陽性だったとしても真の陽性か偽陽性かの区別はつかないので、陽性なら全例インフルエンザとして治療することになります。