
以前アップした記事の続き。
15ゲームは駒の配置によって完成出来る時と出来ない時がある。
どんな場合に出来てどんな場合に出来ないかは、高木貞治著「数学小景」に紹介されていた。

これを読んで今までの疑問が解消した。写真は完成出来る場合の例。
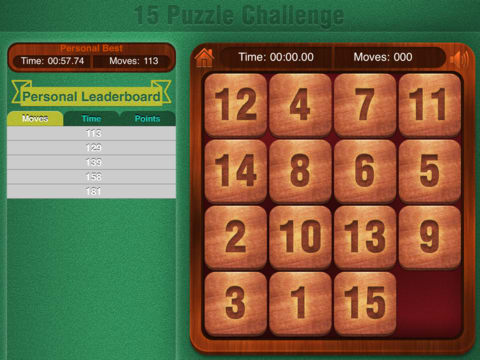
ノートを取りながら読んで、理解した。
このゲームの完成形は、1から15の駒が始めの画像のように並び、16番目
に当たる箇所、右下隅が空所になるという形である。
この形になるための条件は、右下隅が空所になっている状態
の数学の並びが偶順列の時には完成出来るのに対し、
並びが奇順列の時は完成出来ない。
解説途中に置換を使わず、「転倒」という概念を使って
いた。15の駒をランダムに配列した時の
順列の奇偶がゲームの完成と関係があるが、
転倒数の奇偶と順列の奇偶が一致しているので、
こちらを使っている。私は置換を復習したので、
置換の奇偶で理解出来た。
今は転倒数と互換について調べているところだ。

















