お待たせしました、今日はおりがみパヅルの解答編です(え?あんまり待ってない?)。
その前におりがみパヅルがどういうものだったかというと、こちら。

Q.一枚の正方形の紙に切り込みを入れ、11連(11羽)の連鶴を折るものとします。
このとき、
①紙は余らせない
②鶴の翼は必ず別の鶴の翼と繋がっているものとする。頭(嘴)としっぽはいずれにも繋がらない。
とする場合、どのような分割(切り込み)になるか答えなさい。
考案した自分がいうのもなんですが、かなり難しい問題だと思います。
単純に大きな一個の正方形を大きさの異なる十一個の正方形に分割せよ、というだけでなく、さらに連鶴にした場合すべて翼と翼で繋がっているようにしなさいというのですから、ある程度連鶴の概念もわかってないといけないですからね。
自分がこのパズルを思いついたのは、昔、連鶴を嗜んでいた頃、とにかく翼と翼の連結にこだわっていたからです。
連鶴ってただでさえ千切れやすいものなんですが、それが嘴と嘴、嘴としっぽ、嘴と翼というように繋げるとさらに簡単に千切れるんですよね。
千切れたら当然むかつくので、自分は新しい連鶴を創作するときも翼連結のものだけにこだわっていました。
それ(翼連結)にこだわらなければもっとバリエーションが増えますよ~と言ってくれる人もいましたが、それにこだわったからこそ生まれた作品がいくつもある、そう思っています。
前置きが長くなってしまいましたが、これがおりがみパヅル11連の解答です。
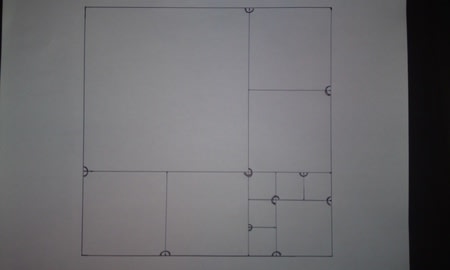
ポイントは二ヶ所の三羽連結ですね。十字のところはつい四羽連結にしてしまいがちですが、それを三羽連結にするのがミソなのです。
この答えで納得してくれるといいけど。汗。
で、実際この分割で連鶴を折ってみるとこうなります。

この画を見て初めて問題の意味がわかったという人も多いはず。笑。
すべての鶴と鶴が翼で繋がっているでしょう?
この分割以外だと、繋がらない翼が出てくるのですよ。
出題は11連でしたが、15連や19連も結構な難問です。
ただ、15連なんかは複数解なんですけどね。
単一解は11連だけなので(4連や8連もそうだけど)、そういった意味で問題に適しているのは11連なのです。
では長々とお付き合いいただきありがとうございました。
自分はパズル作家ではないので、パズルを作成することはまずないのですが、また何か知ら思いついた際はどうかお付き合い下さい。
その前におりがみパヅルがどういうものだったかというと、こちら。

Q.一枚の正方形の紙に切り込みを入れ、11連(11羽)の連鶴を折るものとします。
このとき、
①紙は余らせない
②鶴の翼は必ず別の鶴の翼と繋がっているものとする。頭(嘴)としっぽはいずれにも繋がらない。
とする場合、どのような分割(切り込み)になるか答えなさい。
考案した自分がいうのもなんですが、かなり難しい問題だと思います。
単純に大きな一個の正方形を大きさの異なる十一個の正方形に分割せよ、というだけでなく、さらに連鶴にした場合すべて翼と翼で繋がっているようにしなさいというのですから、ある程度連鶴の概念もわかってないといけないですからね。
自分がこのパズルを思いついたのは、昔、連鶴を嗜んでいた頃、とにかく翼と翼の連結にこだわっていたからです。
連鶴ってただでさえ千切れやすいものなんですが、それが嘴と嘴、嘴としっぽ、嘴と翼というように繋げるとさらに簡単に千切れるんですよね。
千切れたら当然むかつくので、自分は新しい連鶴を創作するときも翼連結のものだけにこだわっていました。
それ(翼連結)にこだわらなければもっとバリエーションが増えますよ~と言ってくれる人もいましたが、それにこだわったからこそ生まれた作品がいくつもある、そう思っています。
前置きが長くなってしまいましたが、これがおりがみパヅル11連の解答です。

ポイントは二ヶ所の三羽連結ですね。十字のところはつい四羽連結にしてしまいがちですが、それを三羽連結にするのがミソなのです。
この答えで納得してくれるといいけど。汗。
で、実際この分割で連鶴を折ってみるとこうなります。

この画を見て初めて問題の意味がわかったという人も多いはず。笑。
すべての鶴と鶴が翼で繋がっているでしょう?
この分割以外だと、繋がらない翼が出てくるのですよ。
出題は11連でしたが、15連や19連も結構な難問です。
ただ、15連なんかは複数解なんですけどね。
単一解は11連だけなので(4連や8連もそうだけど)、そういった意味で問題に適しているのは11連なのです。
では長々とお付き合いいただきありがとうございました。
自分はパズル作家ではないので、パズルを作成することはまずないのですが、また何か知ら思いついた際はどうかお付き合い下さい。



























出題されてから、ずっと考えていました。
頭の中には、11個の正方形で出来た大きな1つの正方形が、いくつもいくつも並びました。
でも、どれも、連鶴になるための条件である「翼が繋がっていること」を満足出来ませんでした。。。
解答を見ました。
とても美しい形で、ボーっとして、「そうかあ、難しい「問い」にはシンプルで美しい「解」がお似合いだなあ・・」なんて考えてました。
とても充実した楽しい日々でした♪
また出題してくださいねっ!
ありがとうございます。
たった一人でもずっと考えていた、そう言ってくれる人がいて、出題した甲斐がありました。
>でも、どれも、連鶴になるための条件である「翼が繋がっていること」を満足出来ませんでした。。。
単純に十一個の正方形に分割するだけなら他にも解がありますが、連鶴にした場合翼が繋がるようにするとなると、記事で紹介した解しかないはずです。
法則を見出したわけではないので、絶対とまでは言い切れませんが…。
>とても美しい形で、ボーっとして、「そうかあ、難しい「問い」にはシンプルで美しい「解」がお似合いだなあ・・」なんて考えてました。
シンプルで美しい解、そう言っていただき嬉しく思います。
我ながらよくこの問題を思いついたなと自画自賛してしまいます。
ほとんどの人には相手にされませんが。笑。
>また出題してくださいねっ!
はい、また何か思いついたときには!
そのときはよろしくお願いしますね!
折鶴って、単体も折り方を含め洗練されていて、発展形態も美しく、奥が深いですね。
はい、本当に折鶴は奥が深いと思います。
連鶴も含め、いろいろ応用が効きますからね。
折鶴抜きでは折り紙そのものが成り立たないといっても過言でははないですよね。