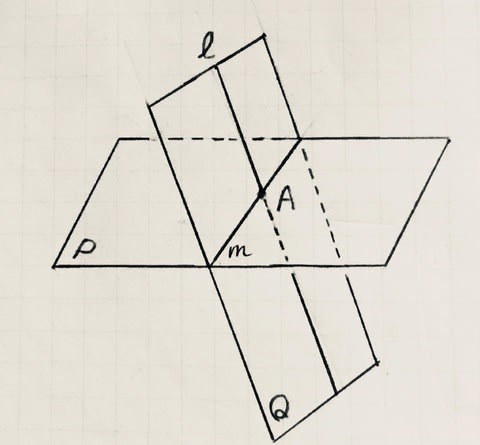
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
2つの直線lとmの交点である。」
このことを証明しなさい。
証明の改良版
交線m上に2点B、Cを取る。

点Aが直線m上にあれば、明らかに命題は成り立つから、
点Aが直線m上にないと仮定する。
この時は点A、B、Cは一直線上にないから、
ただ1つの平面が決まる。
すなわち、この3点を含む平面はただ1つに限る。
ところが仮定より、点Aは直線lと平面Pの交点だから、平面Pと平面Qに含まれ、
点B、Cは平面Pと平面Qの交線だから、これらも平面Pと平面Qに含まれる。
よって、3点A、B、Cは平面Pと平面Qのどちらにも含まれる。
3点A、B、Cを含む平面はただ1つに限るから、
平面Pと平面Qとが一致することになる。
これは平面Pと平面Qとが交わるという仮定に反する。
「点Aが直線m上にない」と仮定すると、「平面Pと平面Qとが交わる」
という命題の仮定に反する矛盾が起こった。
よって点Aが直線m上にないということはあり得ない。
以上から点Aは直線m上にあり、点Aは直線lとmの交点である。
(証明終)

終わり
















