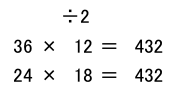xは文字だけれど数を表していることを確認させるために。
==========================================================
80円切手をx枚買いました。さて、いまxが5であるとします。
このとき
80切手を何枚買いましたか?
==========================================================
「5枚」という答えを引き出し、ここまで準備した所で
==========================================================
80円切手をx枚買いました。代金をxの式で表しなさい。
==========================================================
xが3だとします。このとき、何枚買いましたか。代金を求める式は?
・・・・・・
xが7だとします。このとき、何枚買いましたか。代金を求める式は?
x枚買いました。代金を求める式は?
こんなにていねいにやらなくても
80×x
と答えてくれるはず。
80×5=400 とおなじように
80×x=80x と書くことを教える。
このあとは代入の練習をする。
80x=80×x
x=3のとき 80xは何になるかを切手を買う場面
とともに考える。
「このとき」xの値は3になっているから
xのところに3が入れ替わって(代入という)
80x=80×x=80×3=240
を教える。
で、ここでの目的は2x+3という式について考えるため
なので、次は80x+10x、80x+10y、80x+10
の3つの場面を提示する。
つづく
==========================================================
80円切手をx枚買いました。さて、いまxが5であるとします。
このとき
80切手を何枚買いましたか?
==========================================================
「5枚」という答えを引き出し、ここまで準備した所で
==========================================================
80円切手をx枚買いました。代金をxの式で表しなさい。
==========================================================
xが3だとします。このとき、何枚買いましたか。代金を求める式は?
・・・・・・
xが7だとします。このとき、何枚買いましたか。代金を求める式は?
x枚買いました。代金を求める式は?
こんなにていねいにやらなくても
80×x
と答えてくれるはず。
80×5=400 とおなじように
80×x=80x と書くことを教える。
このあとは代入の練習をする。
80x=80×x
x=3のとき 80xは何になるかを切手を買う場面
とともに考える。
「このとき」xの値は3になっているから
xのところに3が入れ替わって(代入という)
80x=80×x=80×3=240
を教える。
で、ここでの目的は2x+3という式について考えるため
なので、次は80x+10x、80x+10y、80x+10
の3つの場面を提示する。
つづく