方程式の指導には結構時間がかかる。
80円切手をx枚買った代金の式80x
封筒に80円切手を貼ってから、10円切手を貼り足した場合の代金
80x+10x
それが90xと等しくなるという理解。
=====================================================================
もし封筒の中身がたくさんあって重かったら・・・、80円では郵便料金が
足りませんね。そういう場合は10円切手を貼り足します。
10円切手は何枚必要ですか?
ここでx枚と答えさせたい。答えなければ、3通の場合は3枚、
4通の場合は・・・と補説を入れます。
x枚ですね。こんな図になります。色がついている方が10円切手です。

切手にかかった代金は全部で
80x+10x
ところがこれは簡単に90xとなりますね。
1通に90円かかるからですね。
したがって 80x+10x=(80+10)x=90xです。
では、10円切手の数を間違えてy枚買ってしまったらどうでしょうか?
=======================================================================
80円切手と90円切手のすべての切手にかかった代金は
80x+90y
となりますが・・・。
90円切手の数が多かった場合、yはxより大きいことになったとき、90円切手は余るので
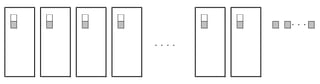
90円切手の数が少なかった場合は

80x+90yは+のない式としてまとまるかというとまとまらないことが分かります。
この生徒は「アルファベットがちがうから一緒にならない」と言っていました。
習ったことを暗記していたようです。
要するに式で表現されたことを具体的なイメージとして持っていることが大事です。
では80x+90は?

イメージはこんな感じです。80円切手x枚と90円切手1枚。
80x+90もまとまらない式。
ここまできて、やっと・・・。
80x+90
にたどり着くことができました。
つづく
80円切手をx枚買った代金の式80x
封筒に80円切手を貼ってから、10円切手を貼り足した場合の代金
80x+10x
それが90xと等しくなるという理解。
=====================================================================
もし封筒の中身がたくさんあって重かったら・・・、80円では郵便料金が
足りませんね。そういう場合は10円切手を貼り足します。
10円切手は何枚必要ですか?
ここでx枚と答えさせたい。答えなければ、3通の場合は3枚、
4通の場合は・・・と補説を入れます。
x枚ですね。こんな図になります。色がついている方が10円切手です。

切手にかかった代金は全部で
80x+10x
ところがこれは簡単に90xとなりますね。
1通に90円かかるからですね。
したがって 80x+10x=(80+10)x=90xです。
では、10円切手の数を間違えてy枚買ってしまったらどうでしょうか?
=======================================================================
80円切手と90円切手のすべての切手にかかった代金は
80x+90y
となりますが・・・。
90円切手の数が多かった場合、yはxより大きいことになったとき、90円切手は余るので

90円切手の数が少なかった場合は

80x+90yは+のない式としてまとまるかというとまとまらないことが分かります。
この生徒は「アルファベットがちがうから一緒にならない」と言っていました。
習ったことを暗記していたようです。
要するに式で表現されたことを具体的なイメージとして持っていることが大事です。
では80x+90は?

イメージはこんな感じです。80円切手x枚と90円切手1枚。
80x+90もまとまらない式。
ここまできて、やっと・・・。
80x+90
にたどり着くことができました。
つづく
















