12と14では一般的ではないので、24と36の場合で説明した。
まず24と36をかけると、(実は864だが計算をしないでおいた)
この数が24と36の公倍数となる。
すなわちその数は
24×36 24の36倍
36×24 36の24倍
である。

この数を2で割ると432になるが、
これはふせて「どちらも同じ数で36の12倍、24の18倍となるでしょ?」ときくと、「はい」
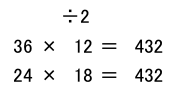
つぎにまだ2で割れるから、割ってあげると
36の6倍、24の9倍という公倍数が見つかる。

さらに3で割ることができて
36の2倍、24の3倍という公倍数が見つかった。

こうして36と24の最小公倍数72が求まる。
まとめると

縦型の計算では

まず2で割る

2×18×12=432

2×2×9×6=216
つぎに3で割る

2×2×3×2=72
今度教えるときは、縦型の計算を教えたい。

おわり
















