３月10日、火曜日。
連日の孫の子守り。
この日は工夫して、
勉強が一段落したところで、DVDを見せる。
お昼は焼き肉。
たっぷり食べた後、１時から１時間、ネット動画。
やがてママがやって来た。いい流れだった。
おばあちゃんも満足。
３月10日、火曜日。
連日の孫の子守り。
この日は工夫して、
勉強が一段落したところで、DVDを見せる。
お昼は焼き肉。
たっぷり食べた後、１時から１時間、ネット動画。
やがてママがやって来た。いい流れだった。
おばあちゃんも満足。
空間図形を復習し出したら、いろいろなことが気になって来た。
図は２平面PとQとの作る角の定義。
２平面の交線l上の点Oを通るP上の垂線mとQ上の垂線nが作る角∠aを
２平面PとQの作る角という。
では、同じように、点O‘と直線m’と直線n‘の作る角∠a’ を作った場合、
∠a’ は∠aに等しいと言えるのか、という疑問。直観的には
等しいといえそうだが、証明は？
３月9日、月曜日。
孫の子守り。
昼食に悩むが、今回は鶏の唐揚げ。
孫たちは喜んで食べたが、その後はネットの動画を見るのに夢中。
我が女房であるおばあちゃんは、孫が相手をしてくれないと、不機嫌だった。
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。
証明の改良版
交線m上に２点B、Cを取る。
点Aが直線m上にあれば、明らかに命題は成り立つから、
点Aが直線m上にないと仮定する。
この時は点A、B、Cは一直線上にないから、
ただ１つの平面が決まる。
すなわち、この3点を含む平面はただ１つに限る。
ところが仮定より、点Aは直線lと平面Pの交点だから、平面Pと平面Qに含まれ、
点B、Cは平面Pと平面Qの交線だから、これらも平面Pと平面Qに含まれる。
よって、3点A、B、Cは平面Pと平面Qのどちらにも含まれる。
3点A、B、Cを含む平面はただ１つに限るから、
平面Pと平面Qとが一致することになる。
これは平面Pと平面Qとが交わるという仮定に反する。
「点Aが直線m上にない」と仮定すると、「平面Pと平面Qとが交わる」
という命題の仮定に反する矛盾が起こった。
よって点Aが直線m上にないということはあり得ない。
以上から点Aは直線m上にあり、点Aは直線lとmの交点である。
（証明終）
終わり
３月８日、日曜日。
公園に散歩に。
その前に神社にお参り。
公園で。いつもの日曜日は野球のチームが練習に来ていたのだが、
コロナウィルスのせいで、グランドにチームの姿がない。
有志が練習していた様子。
いつもの東屋にも将棋のお年寄りの姿がない。
ここで笛の練習が出来た。
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。
証明
交線m上に２点B、Cを取る。
(1) 点B、Cのどちらか一方が点Aと一致する場合は、点Aは直線m上にある。
しかも仮定から、点Aはl上にもあるから、l、mの交点である。
(2) 点B、Cのどちらも点Aと一致しない場合、3点A、B、Cについて、
3点が一直線上にある場合は、点Aは直線m上にあり、(1)と同様に
点Aはl、mの交点である。
(3) ３点が一直線上にない場合、すなわち点Aが直線m上にないとする。
この時は3点A、B、Cによってただ１つの平面が決まる。すなわち
この3点を含む平面はただ１つに限る。
ところが仮定より、点Aは直線lと平面Pの交点だから、平面Pと平面Qにふくまれ、
点B、Cは平面Pと平面Qの交線だから、これらも平面Pと平面Qにふくまれる。
よって、3点A、B、Cは平面Pと平面Qのどちらにもふくまれる。
3点A、B、Cを含む平面はただ１つであるから、
平面Pと平面Qとが一致することになる。
これは平面Pと平面Qとが交わるという仮定に反する。
点Aが直線m上にないと仮定すると、平面Pと平面Qとが交わる
という仮定に反することになるので矛盾が起こった。
よって点Aが直線m上にないということはない。
以上から点Aは直線m上にあり、点Aは直線lとmの交点である。
（証明終）
と、ここまで証明してみたが、よく読み返してみると、
場合分けがくどかった。
(1)と(2)は3点A、B、Cが一直線上にある場合として考えれば、
場合分けは
(1)点Aが直線m上にある場合
(2)点Aが直線m上にない場合
の２つになる。
背理法の証明だから、最初から(2)だけでいいのではないか。
ということで、証明を改良する。
つづく
空間図形の基本はまず公理から。
次の公理を認めて、空間図形の理論を築くのが良い。
公理Ⅰ １直線上にない３点を通る平面はただ１つだけある。
公理Ⅱ 平面上の異なる２点を結ぶ直線上にあるすべての点はこの平面上にある。
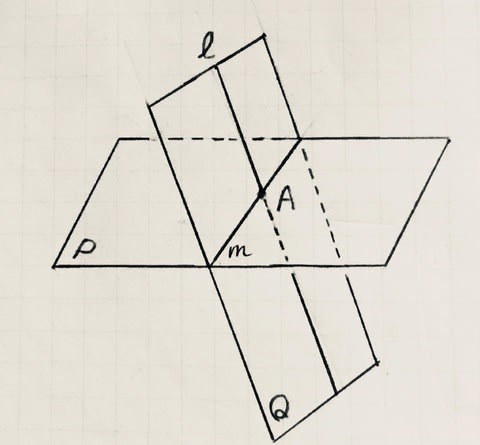
公理Ⅲ ２つの平面はただ１つの共有点持つことはできない。
公理Ⅰと公理Ⅱは理解出来るが、公理Ⅲの効力が今ひとつ不明。
別の本では
公理Ⅰ 平面上の異２点を通る直線は、この平面にふくまれる。
公理Ⅱ １直線上にない３点を通る平面は、１つあって２つとはない。
公理Ⅲ ２つの平面が１点だけを共有することはない。
これらの公理えお基にして、証明を進めて行くわけだ。
空間図形勉強中。
「平面Pと直線lの交点をA。直線lを含む平面Qが平面P
と交わる時にできる交線をmとする。この時、点Aは
２つの直線lとmの交点である。」
このことを証明しなさい。
直観的には明らかなのだが、はたしてそうなのか、
というと不安になる。
そこで証明しようということに。
この性質や証明は手持ちの本にはなかったので、
自力で証明してみた。
証明には空間図形に関する公理が必要だ。これは後日。
数学を職業にしていたので、こんなことも気になる。
つづく
知人からの質問。
メッセージには「イメージがわかない」ということだった。
そこでこの問題に沿って、図を描いて示したところ、下図
「どこが直角三角形になるのか分からない」という。
さらに詳しい図を示して、やっと分かってもらえた。
埼玉県入試と今回のことで感じたのは、
空間図形は１年で学習したっきり、入試問題で突然三平方の定理の応用
として出てくる。本当は理論的にきちんと学べば応用も効くのだが、
一般には直観で解こうとするので、分かりにくいのだと思った。
そこで、発展としてかんたんな空間図形の「定理集」を作ろう
かと思っている。
ところで、論理的に考えたところ、上の図に誤りがあることが分かった。
正しい図はこちら。
空間図形は直観だけに頼らず論理的に考えるのが良いと思う。
