x^2+x+1=0 を解く
1を右辺に移項
x^2+x=-1
両辺に1/2の2乗を加える
x^2+x+(1/2)^2=-1+(1/2)^2
因数分解と計算をする
(x+1/2)^2=-3/4
( )^2=(負の数)
2乗したら負の数になる数、つまり負の数の平方根はない、と中学校では
学んだ。
小学校では「0より小さい数はない」と習ったが、中学校では「ある」と習ったように
中学校では「負の数の平方根はない」と習ったけれども(教えたけれども)、高校では
「ある」と習う。
で、実はある。高校ではこのような数を「虚数」と習う。
x+1/2=±sqrt(-3/4)=±sqrt(-3)/2
と、負の数の平方根を求めしまう。
x=-1/2±sqrt(-3)/2=(-1±sqrt(-3))/2
ここでsqrt(-1)を「虚数単位」といい文字iで表す。
ある数を文字で表すのは円周率π があるが、それと同じように iで表す数がある。
このあと1+3i の様な数を座標平面の(1, 3)で表すことを紹介。
最後にx^3-1=0の3つの解が座標平面で正三角形3つの頂点のように並ぶことを紹介して、授業を終えた。
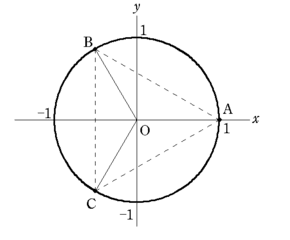
点Aは 1
点Bは (-1+sqrt(3)i)/2
点Cは (-1-sqrt(3)i)/2
もし次にこういう機会があったら、方程式x^5-1=0 の解を紹介して
解を表す点がが正五角形の頂点に並ぶことを示してみたい。
1を右辺に移項
x^2+x=-1
両辺に1/2の2乗を加える
x^2+x+(1/2)^2=-1+(1/2)^2
因数分解と計算をする
(x+1/2)^2=-3/4
( )^2=(負の数)
2乗したら負の数になる数、つまり負の数の平方根はない、と中学校では
学んだ。
小学校では「0より小さい数はない」と習ったが、中学校では「ある」と習ったように
中学校では「負の数の平方根はない」と習ったけれども(教えたけれども)、高校では
「ある」と習う。
で、実はある。高校ではこのような数を「虚数」と習う。
x+1/2=±sqrt(-3/4)=±sqrt(-3)/2
と、負の数の平方根を求めしまう。
x=-1/2±sqrt(-3)/2=(-1±sqrt(-3))/2
ここでsqrt(-1)を「虚数単位」といい文字iで表す。
ある数を文字で表すのは円周率π があるが、それと同じように iで表す数がある。
このあと1+3i の様な数を座標平面の(1, 3)で表すことを紹介。
最後にx^3-1=0の3つの解が座標平面で正三角形3つの頂点のように並ぶことを紹介して、授業を終えた。

点Aは 1
点Bは (-1+sqrt(3)i)/2
点Cは (-1-sqrt(3)i)/2
もし次にこういう機会があったら、方程式x^5-1=0 の解を紹介して
解を表す点がが正五角形の頂点に並ぶことを示してみたい。

















