半径1の円に内接する正五角形の頂点の座標から,円周等分方程式
x^5-1=0 の5つの解が得られます。
図1
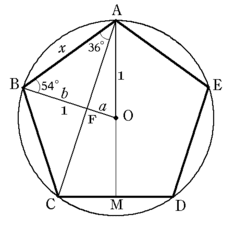
そのために,図1を90度回転させて,座標軸を入れます。
図2

ここでBの座標を求めましょう。Bの座標が求まると,点Bが表す複素数が
求まりますから,円周等分方程式の1つの複素数解が分かります。
Bからx軸に垂線BGを引くと,
△AFO≡△BGO(直角三角形の斜辺と1つの鋭角)
(∵∠F=∠G=90度 斜辺OA=OB ∠Oは共通)
したがって,図2のように,OG=a, GA=b
a=(sqrt(5)-1)/4
BG^2=OB^2-a^2=1-{(sqrt(5)-1)/4}^2=(10+2sqrt(5))/16
BG>0
BG=sqrt(10+2sqrt(5))/4
したがって,x^5-1=0の解のうち,点Bが表す解は
(sqrt(5)-1)/4+i*sqrt(10+2sqrt(5))/4 となる。
数学表記ができる「hatenaブログ」にアップする予定です。
x^5-1=0 の5つの解が得られます。
図1

そのために,図1を90度回転させて,座標軸を入れます。
図2

ここでBの座標を求めましょう。Bの座標が求まると,点Bが表す複素数が
求まりますから,円周等分方程式の1つの複素数解が分かります。
Bからx軸に垂線BGを引くと,
△AFO≡△BGO(直角三角形の斜辺と1つの鋭角)
(∵∠F=∠G=90度 斜辺OA=OB ∠Oは共通)
したがって,図2のように,OG=a, GA=b
a=(sqrt(5)-1)/4
BG^2=OB^2-a^2=1-{(sqrt(5)-1)/4}^2=(10+2sqrt(5))/16
BG>0
BG=sqrt(10+2sqrt(5))/4
したがって,x^5-1=0の解のうち,点Bが表す解は
(sqrt(5)-1)/4+i*sqrt(10+2sqrt(5))/4 となる。
数学表記ができる「hatenaブログ」にアップする予定です。
















