頭の危機

やってしまった。財布の置き忘れ。
学校から駅に向かう途中、財布がないことに気が付いた。家に置き忘れたのだろうと思っていたが、そのうちに昼に郵便局に行ったことを思い出した。振り込みをしたとき、財布があった。
やばい。どこかに忘れた！
慌てて学校に戻った。校舎に入る前に、財布が見付かった！
だめだなー、物忘れが酷すぎる。さては、認知症か…。
とにかく、今日は命拾いをした。(^_^;
財布が見付かったのは不幸中の幸いどころではない。自分の脳は大丈夫なのだろうか…。不安になって来た。

正五角形の探求－２

半径が1の円に内接する正五角形を考えます。その作図方法も考えると、これからの円周等分方程式　x^5-1=0 の解についても考えやすくなります。



こんな感じの五角形。

早速記号などを入れます。



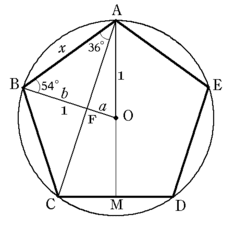
　この五角形をかくには、１辺の長さを求めます。
その長さで円を切っていけばいいのです。
二重根号が出てくるので、式が見づらいですが・・・。
　今回は作図法を・・・・。

円の半径を１とし，正五角形の１辺の長さをxとします。
すると図のように正五角形の性質から
∠BAF=36度，　∠ABF=54度　ですから，∠AFB=90度
つまり，△ABFは直角三角形です。

∠AFOも90度となりますから，△AOF∽△ACM
したがって，AO:AC=OF:CM

正五角形の１辺が１のとき対角線の長さは 1/2(1+sqrt(5))でしたから
正五角形の１辺がxのとき対角線の長さは 1/2(1+sqrt(5))x です。

これより，

1:1/2(1+sqrt(5))x=a:x/2
比の性質から

1:a=1/2(1+sqrt(5))x:x/2=(1+sqrt(5)):1

したがって，　(1+sqrt(5))a=1

これから， a=1/(1+sqrt(5))

分母を有理化すると　　a=(sqrt(5)-1)/4

△ABFで
x^2=AB^2=BF^2+AF^2

ここでBF^2=b^2=(1-a)^2={(5-sqrt(5))/4}^2

AF^2=1^2-a^2=1-{(sqrt(5)-1)4}^2

x^2={(5-sqrt(5))/4}^2+1-{(sqrt(5)-1)4}^2
=(5-sqrt(5))/2

x^2=(5-sqrt(5))/2=(10-2sqrt(5))/4　より

x=sqrt(10-2sqrt(5))/2

これでxは求まりましたが，問題はxの長さの作図法です。

それには，次のようにします。

x^2=(5-sqrt(5))/2=1+(3-sqrt(5))/2=1+(6-2sqrt(5))/4

ここで(6-2sqrt(5))/4={(sqrt(5)-1/2}^2 ですから

x^2=1^2+{(sqrt(5)-1)/2}^2

となります。するとxは直角をはさむ２辺が
1と(sqrt(5)-1)/2である直角三角形の斜辺として求められます。
実際の作図では次のようになります。

　

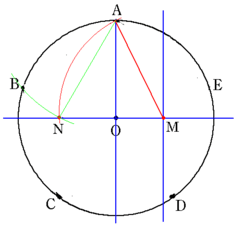
半径１の円で，まず円周上に１点Aをとります。直径OAと垂直な直径（水平線）を引きます。
OM=1/2に取ります。垂直二等分線の作図でMは求まります。
このときMA=sqrt(5)/2 です。
Mを中心として，MAを半径とする円と水平線との交点をNとすると
ON=NM-OM=sqrt(5)/2-1/2=(sqrt(5)-1)/2

正五角形の１辺の長さxは
x^2=1^2+{(sqrt(5)-1)/2}^2　であり，
xは直角をはさむ２辺が
1と(sqrt(5)-1)/2である直角三角形の斜辺として求められますから

ANが求める長さxとなります。
図はAN=ABとして，点Bを求めたところです。あとは点C，D，E
をとれば良いのです。